Mean Value Theorem

中學純數，以及大學微積分課程，我也學過 Mean Value Theorem:
If f(x) is continuous on [a, b] and differentiable on (a, b), then there is a c in (a, b) such that

f'(c)= [f(b)-f(a)]/(b-a)

它的幾何意義，就是說出若 y=f(x) 是區間 [a,b] 上的一條圓滑曲線，則存在一點 (c, f(c))，在該點上的切線斜率會等於連接 (a, f(a)) 和 (b, f(b))的直線斜率。



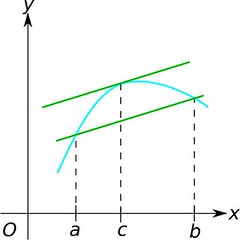
此外，還學了一個叫 General mean value theorem:
If f(x) and g(x) are continuous on [a, b] and differentiable on (a, b), then there is a c in (a, b) such that
f'(c)[g(b)-g(a)] = g'(c)[f(b)-f(a)]
幾年來，我一直也想不出它的幾何意義，證明時又要砌多一個函數來搞。
近日看了一些幾何書籍，搞幾何時多數不會用 y=f(x) 的形式去表示曲線方程，而是用參數式 ( x(t), y(t) ) 來表示。

用參數式去看 mean value theorem 的幾何意義，所得的數式不就是 general mean value theorm 的形式嗎？

大一 calculus 已是多年前的事，現今才知道這個意義，看來我真是無乜料。

人又不夠勤力吧。想出這個意義後，我上 wiki 到看看，原來也有記述這個詮釋。勤力d睇多幾本書，或者我已經一早知道。

遲就遲d，但自己親手解決多年的疑惑，是一件十分喜悅的事情。