哥德爾不完備定理 (Gödel's incompleteness theorems) 是一條有關數理邏輯的重要定理,說實話,我絕對談不上認識這條定理,不過有些感想想與大家談談。
古希臘歐幾里得幾何,由一小撮基本定義 (definition) 和公理 (axiom),證明出新的定理 (theorem)。而藉由定義、公理和定理,亦可證明千千萬萬更多新的定理。
一套很完善的系統吧?除了歐氏幾何外,其他數學能否以這種邏輯體系表現出來?十九、二十世紀的數學家,如康德 (Georg Cantor)、羅素 (Bertrand Russell) 等在數學基礎上作出了很大的努力,例如集合論的創立等。後來希伯特 (David Hilbert) 提出了希伯特計劃 (Hilbert's project)。希爾伯特計劃,是想以形式系統 (formal system) 來表現數學,即是希望以有限的公理作為數學根基,並希望能證明出這種系統是相容 (consistent) 和完備 (complete) 的。
相容和完備是兩個很重要的概念,亦是我們追求的理想境界。何謂相容?何謂完備呢?
相容的意思,是指在系統內合法的推理下不會推導出矛盾的結果。例如「我是男人」及「我不是男人」這兩個命題不可能均被證明為真的。
而完備的意思,是指系統內的命題均可被證明。
因此,在一個「相容」兼「完備」的系統內,「我是男人」及「我不是男人」中,只少有一個命題可被證明為真。
大家試想一想,如果系統不相容,推導出來的結果並不可靠。如果不完備,便要接受有些結果是無法被證明出來。同時具備相容及完備,那真是最好不過呢!
但在1930年代,哥德爾 (Kurt Gödel) 的兩條不完備定理,否定了希伯特計劃。
簡單來說,第一不完備定理指出滿足某條件的相容形式系統中,會有在該系統中不能被證明的命題,即是不完備,而第二不完備定理指出滿足某條件的相容系統不能由該系統證明自身的相容性。
當中的「某條件」,我不在此多加解釋。但注意,不完備定理是應容於滿足「某條件」的系統。確會存在既相容又完備的系統,例如兩千多年前歐幾里得的歐氏幾何,補上一些基本的公理後是一個完備又相容的系統。但並不是所有系統均可這樣做。
數學,講到這樣。大家已經悶死吧?
追求相容的同時,原來要犧牲當中的完備性。完美是不存在吧?至少在某條件之下……
活在當下,我們不得不承認有些東西是做不來、做不到。盲目追求完美,其實是一件虛無飄渺的事情,但這不代表我們做事求求其其便可,人生過得求求其其亦可。在一些框架下,總有很多東西可以做,在此框架下把事情做好。但事情都未做好,甚至未開始去做,便去想如何做到「最」好,做到「完美」,是否不切實際呢?
**********************************************************
這篇粗疏的文章,可能當中會有錯漏,請見諒。如果大家對哥德爾不完備定理有興趣,我有些書籍可以推介一下:
1. 《數學女孩 -- 哥德爾不完備定理》,作者為結成浩。
結成浩這個數學女孩系列,日本已出版了五冊,台灣世茂翻譯了四冊。這是一部數學小說,每冊都以通俗易懂的手法由淺入深帶出最後該冊的主題。不過在哥德爾不完備定理,最後一章是要帶出該該定理的證明,我功力有限看不懂呢 :P
另外,世茂這個系列,翻譯常有出錯。不過我又不懂日文,不知原版如何。
2. Godel's Proof, by Ernest Nagel
http://www.amazon.com/G%C3%B6dels-Proof-Ernest-Nagel/dp/0814758371
這本小書不是小說形式,但也算易懂,香港誠品也見有售。我懷疑數學女孩中的一些鋪排也是參考此書。
**********************************************************
本文同步於 http://11235813.wikidot.com/blog:20130908-godel 發表
Showing posts with label math. Show all posts
Showing posts with label math. Show all posts
Sunday, September 08, 2013
Sunday, May 26, 2013
有關多面體的一則無聊對談
H:你知道這是甚麼嗎?
J:骰子
H:不是呀,我指這是甚麼形狀?
J:你知咩
H:正十二面體呀
J:你又知有十二個面
H:唔信你數下吧
J:咁英文係乜呀
H:Dodecahedron
J:咩話?
H:Dodecahedron
J:哦,BoBeBaLeon
H:唔係呀,係Dodecahedron
J:我咪話GoGeDaAeon 囉!
H: ~.~
J:點解係正呀
H:D邊一樣長,四四正正咁
J:咁係等邊,等邊咪等邊囉,搞咁多野
……
其實這個「正」,確是「四四正正」咁解,四正的表現,除了等邊,還有等角,即所有面皆是正多邊形!更甚者,你從任何一個頂點去觀察,這個立體的投影也是一樣的!
……
J:咁你知唔知正十三面體英文係乜?
H:唔知呢,願聞其詳!
J:就是 WoLaBaKeon
H:傻妹,無正十三面體架
J:點解無呀?
H:總之係無啦。
J:咁下一個正XX面體係乜?
H:正二十面體,Icosahedron
J:我咪就係話 YoGaSaVeon!
H: >.<
……
正多面體,如果只計凸正多面體,其實只有五種:正四面體、正六面體、正八面體、正十二面體、正二十面體。
哈哈,不過中文的命名,又確易令人有這想法。有正五邊形正六邊形正七邊形……去到立體的情況,有正十二面體為何會沒有正十三面體呢?
哈哈哈哈
點解?參看小弟之前寫的文章:
http://deadfatboy.blogspot.hk/2009/05/blog-post_17.html
http://deadfatboy.blogspot.hk/2009/05/2.html
J:骰子
H:不是呀,我指這是甚麼形狀?
J:你知咩
H:正十二面體呀
J:你又知有十二個面
H:唔信你數下吧
J:咁英文係乜呀
H:Dodecahedron
J:咩話?
H:Dodecahedron
J:哦,BoBeBaLeon
H:唔係呀,係Dodecahedron
J:我咪話GoGeDaAeon 囉!
H: ~.~
J:點解係正呀
H:D邊一樣長,四四正正咁
J:咁係等邊,等邊咪等邊囉,搞咁多野
……
其實這個「正」,確是「四四正正」咁解,四正的表現,除了等邊,還有等角,即所有面皆是正多邊形!更甚者,你從任何一個頂點去觀察,這個立體的投影也是一樣的!
……
J:咁你知唔知正十三面體英文係乜?
H:唔知呢,願聞其詳!
J:就是 WoLaBaKeon
H:傻妹,無正十三面體架
J:點解無呀?
H:總之係無啦。
J:咁下一個正XX面體係乜?
H:正二十面體,Icosahedron
J:我咪就係話 YoGaSaVeon!
H: >.<
……
正多面體,如果只計凸正多面體,其實只有五種:正四面體、正六面體、正八面體、正十二面體、正二十面體。
哈哈,不過中文的命名,又確易令人有這想法。有正五邊形正六邊形正七邊形……去到立體的情況,有正十二面體為何會沒有正十三面體呢?
哈哈哈哈
點解?參看小弟之前寫的文章:
http://deadfatboy.blogspot.hk/2009/05/blog-post_17.html
http://deadfatboy.blogspot.hk/2009/05/2.html
Saturday, November 17, 2012
比例代表制,與2012年立法會選舉隨想
幾年前曾寫過一篇有關比例代表制的文章:
http://deadfatboy.blogspot.hk/2008/08/blog-post_31.html
在2012立法會選舉後,本來也想多寫一文,不過一直沒有空,最近才完成。內裏有些少數學討論,請到以下連結一看:
http://11235813.wikidot.com/others:20121117-vote2012
http://deadfatboy.blogspot.hk/2008/08/blog-post_31.html
在2012立法會選舉後,本來也想多寫一文,不過一直沒有空,最近才完成。內裏有些少數學討論,請到以下連結一看:
http://11235813.wikidot.com/others:20121117-vote2012
Tuesday, January 03, 2012
逆反命題
剛入大學時,有一科叫 Linear Algebra I,開學時所講的全不是數學,而是集合與邏輯。當時我覺得既抽象又沉悶,但其實這才是畢生受用的東西。
學習 propositional calculus 時,覺得逆反命題 (contraposition)實在難明,當中的充分條件、必要條件,搞到一頭霧水。有時像明白了,但又好似不懂去運用。不過隨著往後幾年的物理和數學訓練,這些邏輯慢慢也搞通了。
我覺得生活上很多謬誤,是源於對逆反命題的誤解。
看看以下命題:
「若P,則Q。」
它的逆反命題便是:
「若非Q,則非P。」
邏輯上,只要原命題為真,它的逆反命題也必為真。例如:
「若我在香港生活,則我在中國生活。」
這個是真命題。它的逆反命題為:
「若我不在中國生活,則我不在香港生活。」
由於原命題為真,以上命題也為真。
但留意以下兩個命題皆不是原命題的逆反命題。
1. 「若我不在香港生活,則我不在中國生活。」(若非P,則非Q。)
2. 「若我在中國生活,則我在香港生活。」(若Q,則P。)
命題1是原命題的反命題(inversion),而命題2是原命題的逆命題(conversion)。邏輯上,原命題為真並不保證它的反命題和逆命題為真。
但是,很多時人們也會錯以為反命題和逆命題為真!
我覺得無論宗教也好,政治也好,很多事端其實也源於人們對逆反命題的誤解,或是有心人故意製造這種誤解。
在馬克斯的共產思想中,他認為「若實行資本主義,則會導治失業問題。」
假設馬克斯的理論正確,以上便是真命題,它的逆反命題為:「若要解決失業問題,則不可實行資本主義。」
就是如此,只是如此。
但是,不知是有心還是無意,人們將之曲解為「若不實行資本主義,則可解決失業問題。」,於是進入火紅年代,在世上翻起了千呎巨浪……
馬克斯並沒有錯,他可沒有保證不實行資本主義則可解決失業問題呢!
學習 propositional calculus 時,覺得逆反命題 (contraposition)實在難明,當中的充分條件、必要條件,搞到一頭霧水。有時像明白了,但又好似不懂去運用。不過隨著往後幾年的物理和數學訓練,這些邏輯慢慢也搞通了。
我覺得生活上很多謬誤,是源於對逆反命題的誤解。
看看以下命題:
「若P,則Q。」
它的逆反命題便是:
「若非Q,則非P。」
邏輯上,只要原命題為真,它的逆反命題也必為真。例如:
「若我在香港生活,則我在中國生活。」
這個是真命題。它的逆反命題為:
「若我不在中國生活,則我不在香港生活。」
由於原命題為真,以上命題也為真。
但留意以下兩個命題皆不是原命題的逆反命題。
1. 「若我不在香港生活,則我不在中國生活。」(若非P,則非Q。)
2. 「若我在中國生活,則我在香港生活。」(若Q,則P。)
命題1是原命題的反命題(inversion),而命題2是原命題的逆命題(conversion)。邏輯上,原命題為真並不保證它的反命題和逆命題為真。
但是,很多時人們也會錯以為反命題和逆命題為真!
我覺得無論宗教也好,政治也好,很多事端其實也源於人們對逆反命題的誤解,或是有心人故意製造這種誤解。
在馬克斯的共產思想中,他認為「若實行資本主義,則會導治失業問題。」
假設馬克斯的理論正確,以上便是真命題,它的逆反命題為:「若要解決失業問題,則不可實行資本主義。」
就是如此,只是如此。
但是,不知是有心還是無意,人們將之曲解為「若不實行資本主義,則可解決失業問題。」,於是進入火紅年代,在世上翻起了千呎巨浪……
馬克斯並沒有錯,他可沒有保證不實行資本主義則可解決失業問題呢!
Saturday, November 05, 2011
台灣小四數學題太難
大家想想以下題目:
A、B 兩數相乘。某人把 A 的十位數字 1 看成 7,乘積多了 4140;另一人把 B 的十位數字 6 看成 4,乘積少了 2240。正確的乘積到底是多少?
這是台灣小四的習題,據聞連家長也難倒要在網上求教。
我在這兒出的數學文章通常也無人會睇,甚至有人叫我收皮,後來我開設了 11235813.wikidot.com ,便很少在這兒出數學文章。這題目的前因後果,令我有不少感想,我都希望大家有空的話可以過去看看:
http://11235813.wikidot.com/others:20111104-taiwan-p4-math-problem
順便在這兒拉拉客仔,哈哈哈,這邊的瀏覽量低,那邊便是極低 :D
A、B 兩數相乘。某人把 A 的十位數字 1 看成 7,乘積多了 4140;另一人把 B 的十位數字 6 看成 4,乘積少了 2240。正確的乘積到底是多少?
這是台灣小四的習題,據聞連家長也難倒要在網上求教。
我在這兒出的數學文章通常也無人會睇,甚至有人叫我收皮,後來我開設了 11235813.wikidot.com ,便很少在這兒出數學文章。這題目的前因後果,令我有不少感想,我都希望大家有空的話可以過去看看:
http://11235813.wikidot.com/others:20111104-taiwan-p4-math-problem
順便在這兒拉拉客仔,哈哈哈,這邊的瀏覽量低,那邊便是極低 :D
Monday, August 29, 2011
百分法的誤用
臨近開學,新聞又話今年學生開學洗費比往年貴。
在這個通脹環境下,開學洗費比往年貴是正常不過了,如果乜都貴,開學洗費反而比往年便宜,那才是一反常態值得大家深思吧?
既然貴是理所當然,咁又有乜好UP?當中有乜亮點?當然要誇張啦。
剛剛收看無線《東張西望》(8月29日),內裏有個個案,訪問了一個中三女生,看看她今年的開學洗費,結論是比去年大幅上升兩倍。大家是否覺得很驚訝?
我十分驚訝,立即由聽電視變為看電視,銀幕上閃出了兩張清單,分別是去年的開學洗費與今年的開學洗費。
在去年,有以下兩個項目:
教科書
文具
合共二千多元
而今年,有以下數個項目:
教科書
文具
書包
校服
(不知有沒有遺漏,畫面實在閃得太快)
合供四千多元
單是校服便千多元!這個項目在去年是沒有的。相信不用我去解釋,大家也看出內裏玄機吧。
原來這樣也可以作出比較,真是看得我目定口呆。
如果大家沒有看畫面,只聽旁述,真的會給「上升兩倍」嚇破膽!
何必要咁呢?真的無新聞嗎?
各位數學科老師,好應該上 MyTV 下載該節目,作為日後的教材。
在這個通脹環境下,開學洗費比往年貴是正常不過了,如果乜都貴,開學洗費反而比往年便宜,那才是一反常態值得大家深思吧?
既然貴是理所當然,咁又有乜好UP?當中有乜亮點?當然要誇張啦。
剛剛收看無線《東張西望》(8月29日),內裏有個個案,訪問了一個中三女生,看看她今年的開學洗費,結論是比去年大幅上升兩倍。大家是否覺得很驚訝?
我十分驚訝,立即由聽電視變為看電視,銀幕上閃出了兩張清單,分別是去年的開學洗費與今年的開學洗費。
在去年,有以下兩個項目:
教科書
文具
合共二千多元
而今年,有以下數個項目:
教科書
文具
書包
校服
(不知有沒有遺漏,畫面實在閃得太快)
合供四千多元
單是校服便千多元!這個項目在去年是沒有的。相信不用我去解釋,大家也看出內裏玄機吧。
原來這樣也可以作出比較,真是看得我目定口呆。
如果大家沒有看畫面,只聽旁述,真的會給「上升兩倍」嚇破膽!
何必要咁呢?真的無新聞嗎?
各位數學科老師,好應該上 MyTV 下載該節目,作為日後的教材。
Tuesday, February 08, 2011
NUMB3RS
最近,我在追看一套美國電視劇,名為 NUMB3RS。看劇名,大家都應該估到這電視劇是和數學有關吧?是的,這是一套用數學來做包裝的警匪片。
劇中,主角 Don 是一個 FBI 探員。他的弟弟 Charlie 是一位在 CalSci 任教的年青數學教授,研究應用數學。好奇底下,Charlie 用數學幫 Don 去研究案情,後來甚至成為 FBI 的 Consultant,協助 Don 去查案。還有 Charlie 的亦師亦友,物理教授 Larry (研究 Cosmology),以及 Charlie 的學生(後來是情侶) Amita,也有協助以 Don 為首的一隊 FBI 去破案。
(CalSci 是劇中一所虛構的大學,片中很多該學校的場景是取自 CalTech。)
每集約四十分鐘,都是由一個案件帶起,借助數學去解決,看到數學咁有用,都幾高興。還有槍林彈雨,緊張刺激呢!
身邊很多朋友都有追看 Big Bang Theory,但別以為 NUMB3RS 與 Big Bang Theory 同屬搞笑劇種,NUMB3RS 嚴肅得多,查案和數學也頗認真的。某些單元會較合理,某些單元我覺得較為牽強,或許是因為我的數學知識貧乏。
為了視覺效果,某些東西很明顯是被誇大了。例如漂亮的程式介面、Charlie 在黑版上的運算……講真,我唔相信有人可以對那些高等數學進行心算……
看了十多集,真係不得不承認概率論的應用之廣,不止一次出現過 Bayseian statistics 。也不得不服編劇的腦汁,連 Riemann Hypothesis 也可容入故事之中!
在首季開始無幾耐有一集,我印象很深。Charlie 為某案件設計了一個數學模型,他認為當中的數學是沒有錯,但就是不能解決問題,很心灰。Larry 給了他一些提議:數學係完美,但人不是完美,你要在模型中加入人的不完美才行。還有一集,Larry 提點 Charlie,你往往根據你的假設去做,有沒有想過可能你的假設是有問題?
這兩點,我很大個先領略得到。一直以來我們學習階段的數學習題,盡是完美的。所給的資料不會多,也不會少,只要你沒有推論錯誤,就一定可以期待著一個完美的答案出現在面前。但我們的現實並不是這樣,要用數學來解決真真正正的現實問題也不是這樣。資料,要自己去找;假設,也要自己去建立。現實的不完美,要令我們作出更多「合情」的假設,但「合情」不等於邏輯上的真確,但也未必不可用來解決問題呢。
用數學來解決現實生活的問題,這工作實在刺激,令我很羨慕呢。
煲完第一季,竟然買不到第二季和第三季,一下子跳到去第四季,發覺當中斷纜了,唯有在 Wiki 看一些資料簡介吧。
劇中,主角 Don 是一個 FBI 探員。他的弟弟 Charlie 是一位在 CalSci 任教的年青數學教授,研究應用數學。好奇底下,Charlie 用數學幫 Don 去研究案情,後來甚至成為 FBI 的 Consultant,協助 Don 去查案。還有 Charlie 的亦師亦友,物理教授 Larry (研究 Cosmology),以及 Charlie 的學生(後來是情侶) Amita,也有協助以 Don 為首的一隊 FBI 去破案。
(CalSci 是劇中一所虛構的大學,片中很多該學校的場景是取自 CalTech。)
每集約四十分鐘,都是由一個案件帶起,借助數學去解決,看到數學咁有用,都幾高興。還有槍林彈雨,緊張刺激呢!
身邊很多朋友都有追看 Big Bang Theory,但別以為 NUMB3RS 與 Big Bang Theory 同屬搞笑劇種,NUMB3RS 嚴肅得多,查案和數學也頗認真的。某些單元會較合理,某些單元我覺得較為牽強,或許是因為我的數學知識貧乏。
為了視覺效果,某些東西很明顯是被誇大了。例如漂亮的程式介面、Charlie 在黑版上的運算……講真,我唔相信有人可以對那些高等數學進行心算……
看了十多集,真係不得不承認概率論的應用之廣,不止一次出現過 Bayseian statistics 。也不得不服編劇的腦汁,連 Riemann Hypothesis 也可容入故事之中!
在首季開始無幾耐有一集,我印象很深。Charlie 為某案件設計了一個數學模型,他認為當中的數學是沒有錯,但就是不能解決問題,很心灰。Larry 給了他一些提議:數學係完美,但人不是完美,你要在模型中加入人的不完美才行。還有一集,Larry 提點 Charlie,你往往根據你的假設去做,有沒有想過可能你的假設是有問題?
這兩點,我很大個先領略得到。一直以來我們學習階段的數學習題,盡是完美的。所給的資料不會多,也不會少,只要你沒有推論錯誤,就一定可以期待著一個完美的答案出現在面前。但我們的現實並不是這樣,要用數學來解決真真正正的現實問題也不是這樣。資料,要自己去找;假設,也要自己去建立。現實的不完美,要令我們作出更多「合情」的假設,但「合情」不等於邏輯上的真確,但也未必不可用來解決問題呢。
用數學來解決現實生活的問題,這工作實在刺激,令我很羨慕呢。
煲完第一季,竟然買不到第二季和第三季,一下子跳到去第四季,發覺當中斷纜了,唯有在 Wiki 看一些資料簡介吧。
Saturday, November 06, 2010
Conditional Probability
Conditional Probability,中譯「條件概率」。中學時大家也學過吧?忘了是甚麼?看看以下示例:
某袋內有 8 個紅球、2 個白球。從袋裏逐一隨機抽出 2 個球,且抽出的球不放回袋中 (without replacement)。已知第一個抽出的是紅球,求第二個抽出的是紅球的概率。
答案當然不是 8/10,第二次抽球的結果的概率會受第一次抽球的結果影響。
因為第一個抽出的是紅球,所以袋裏剩下 7 個紅球和 2 個白球。因此,答案是 2/9。
這例子中所求的便是一個條件概率。
已知事件 A 發生的情況下求事件 B 的概率,這是一個條件概率,以符號 P(B|A) 表示。
在我讀中四、五的年代,沒有引入 P(B|A) 這符號。在以上例子,如果要求抽出兩個紅球的概率,就會這樣寫出來:
P(兩個紅球)
=P(R1)*P(R2)
=(8/10)*(7/9)
=28/45
但情況如果變為「抽出的球會放回袋中」,即是 "with replacement",寫法依舊,但數字不同:
P(兩個紅球)
=P(R1)*P(R2)
=(8/10)*(8/10)
=16/25
老師也不會提甚麼條件概率,總之心入面知道是 with replacement 還是 without replacement,寫出正確的乘式便行。那時也不需要學習以下公式:
P(A|B) = P(A and B)/P(B)
不過於早幾年(2006)的會考數學課程中,也引入了條件概率的概念及以上公式。於是以上抽球問題,便可列式如下:
P(兩個紅球)
=P(R1)*P(R2|R1)
=(8/10)*(7/9)
=28/45
這樣有一個好處,就是要求學生更注意涉及的事件是否「相關事件」(dependent events),如在上例的抽球問題,球是否須放回袋中。
不過我個人覺得,要學習那個條件概率的公式,以我過往的學習經驗來說,我覺得幾深,可能是我自己習不得其法。
那公式,是我到中六應用數學課程中才接觸。那時意會到,原來過往抽球中不把球放回所計算的,是一個條件概率,去到這裏也沒有甚麼大問題。但再學那條公式,問題就出現了。
這個不是數學問題,是我個人的感觀問題。
「已知事件 A 發生,求事件 B 發生的概率。」
無問題呀,把數字代入公式便可。我搞得清哪事件是已知,要求哪事件的概率,無問題呀。
再以以上抽球的例子,有時習題可能會這樣問:
(a) 已知第一個抽出的是紅球,求第二個抽出的是紅球的概率。
(b) 已知第二個抽出的是紅球,求第一個抽出的是紅球的概率。
(a) 沒有甚麼問題。但那時候 (b) 簡直令我瘋顛。當時我在想,既然知道第二個抽出的是紅球,你不抽第一個球,哪會去抽第二個球?已抽了第一個球,即是知道它是甚麼顏色,為何要求概率?
相信大家都看到,我那時的 Mathematics maturity 或者太低。
這情況聽落很怪,但這種「已知………發生,求………發生的概率」,其實係數學上係 well defined object,按定義去做便行,實在想得太多了。那時候我糾結於現實中的「先」和「後」,令我對條件概率很迷惑。
其實應該放開先後的概念,不過我見過不少文獻在講授條件概率時也有用到先後的概率,例如這樣定義:
在事件 B 已經發生的情況下事件 A 發生的概率。
不知會唔會有學生出現與我一樣的困惑?
我覺得這樣講較好
在事件 B 發生的情況下事件 A 發生的概率。
而事實上,亦不是已發生的就是肯定的,早前作題目,我想過一個例子。
會考中的多項選擇題,某條有多少百分比的學生選了A、多少選了B、多少選了C、多少選了D,這些資料考試局是有齊的。知道有幾多幾多百分比的學生選中正確答案又如何?學生可以瞎猜吧!無錯,學生是可以瞎猜,但你也可以從這些資料估計出真正有多少學生知道正確答案。
如果某條多項選擇題有四個選擇,結果有 80% 的考生選中。現在看看究竟真正有多少人真正知道該題的答案。當然,事前我要作出一些合理的假設。我假設知道正確答案的必會選出正確選項,不知答案的必會從四個選項中隨機選一個。
設 A 為學生知道正確答案的事件,B 為學生選出正確答案的事件。
設 x% 的考生知道正確答案。
於是
P(B)= P(A)*P(B|A)+P(not A)*P(B|notA)
80% = (x%)*(1)+(1-x%)(1/4)
得出 x = 73.333333....
這個才是 80% 背後的意義。我們本身無法知道真正有多少學生知道正確答案,但就可以用條件概率去作估計。
這類例子,一般講解條件概率的書籍皆有提及,例如檢驗某病毒等例子,但甚少會再去討論當中的用意,其價值貶為一般示例。
或者只是基於我的無知而小提大做吧。
不過,條件概率實在是概率論中一個很強的工具,一定要好好理解。
某袋內有 8 個紅球、2 個白球。從袋裏逐一隨機抽出 2 個球,且抽出的球不放回袋中 (without replacement)。已知第一個抽出的是紅球,求第二個抽出的是紅球的概率。
答案當然不是 8/10,第二次抽球的結果的概率會受第一次抽球的結果影響。
因為第一個抽出的是紅球,所以袋裏剩下 7 個紅球和 2 個白球。因此,答案是 2/9。
這例子中所求的便是一個條件概率。
已知事件 A 發生的情況下求事件 B 的概率,這是一個條件概率,以符號 P(B|A) 表示。
在我讀中四、五的年代,沒有引入 P(B|A) 這符號。在以上例子,如果要求抽出兩個紅球的概率,就會這樣寫出來:
P(兩個紅球)
=P(R1)*P(R2)
=(8/10)*(7/9)
=28/45
但情況如果變為「抽出的球會放回袋中」,即是 "with replacement",寫法依舊,但數字不同:
P(兩個紅球)
=P(R1)*P(R2)
=(8/10)*(8/10)
=16/25
老師也不會提甚麼條件概率,總之心入面知道是 with replacement 還是 without replacement,寫出正確的乘式便行。那時也不需要學習以下公式:
P(A|B) = P(A and B)/P(B)
不過於早幾年(2006)的會考數學課程中,也引入了條件概率的概念及以上公式。於是以上抽球問題,便可列式如下:
P(兩個紅球)
=P(R1)*P(R2|R1)
=(8/10)*(7/9)
=28/45
這樣有一個好處,就是要求學生更注意涉及的事件是否「相關事件」(dependent events),如在上例的抽球問題,球是否須放回袋中。
不過我個人覺得,要學習那個條件概率的公式,以我過往的學習經驗來說,我覺得幾深,可能是我自己習不得其法。
那公式,是我到中六應用數學課程中才接觸。那時意會到,原來過往抽球中不把球放回所計算的,是一個條件概率,去到這裏也沒有甚麼大問題。但再學那條公式,問題就出現了。
這個不是數學問題,是我個人的感觀問題。
「已知事件 A 發生,求事件 B 發生的概率。」
無問題呀,把數字代入公式便可。我搞得清哪事件是已知,要求哪事件的概率,無問題呀。
再以以上抽球的例子,有時習題可能會這樣問:
(a) 已知第一個抽出的是紅球,求第二個抽出的是紅球的概率。
(b) 已知第二個抽出的是紅球,求第一個抽出的是紅球的概率。
(a) 沒有甚麼問題。但那時候 (b) 簡直令我瘋顛。當時我在想,既然知道第二個抽出的是紅球,你不抽第一個球,哪會去抽第二個球?已抽了第一個球,即是知道它是甚麼顏色,為何要求概率?
相信大家都看到,我那時的 Mathematics maturity 或者太低。
這情況聽落很怪,但這種「已知………發生,求………發生的概率」,其實係數學上係 well defined object,按定義去做便行,實在想得太多了。那時候我糾結於現實中的「先」和「後」,令我對條件概率很迷惑。
其實應該放開先後的概念,不過我見過不少文獻在講授條件概率時也有用到先後的概率,例如這樣定義:
在事件 B 已經發生的情況下事件 A 發生的概率。
不知會唔會有學生出現與我一樣的困惑?
我覺得這樣講較好
在事件 B 發生的情況下事件 A 發生的概率。
而事實上,亦不是已發生的就是肯定的,早前作題目,我想過一個例子。
會考中的多項選擇題,某條有多少百分比的學生選了A、多少選了B、多少選了C、多少選了D,這些資料考試局是有齊的。知道有幾多幾多百分比的學生選中正確答案又如何?學生可以瞎猜吧!無錯,學生是可以瞎猜,但你也可以從這些資料估計出真正有多少學生知道正確答案。
如果某條多項選擇題有四個選擇,結果有 80% 的考生選中。現在看看究竟真正有多少人真正知道該題的答案。當然,事前我要作出一些合理的假設。我假設知道正確答案的必會選出正確選項,不知答案的必會從四個選項中隨機選一個。
設 A 為學生知道正確答案的事件,B 為學生選出正確答案的事件。
設 x% 的考生知道正確答案。
於是
P(B)= P(A)*P(B|A)+P(not A)*P(B|notA)
80% = (x%)*(1)+(1-x%)(1/4)
得出 x = 73.333333....
這個才是 80% 背後的意義。我們本身無法知道真正有多少學生知道正確答案,但就可以用條件概率去作估計。
這類例子,一般講解條件概率的書籍皆有提及,例如檢驗某病毒等例子,但甚少會再去討論當中的用意,其價值貶為一般示例。
或者只是基於我的無知而小提大做吧。
不過,條件概率實在是概率論中一個很強的工具,一定要好好理解。
Sunday, September 05, 2010
101010
101010,這一組數字今年可有多重意義。
10/10/10,中華民國建國九十九週年,首次出現「三十節」。(惡搞,速逃,哈哈哈~~~)
以前臨近雙十節,香港都有不少地方會掛起青天白日旗。現今香港回歸後,當然不會有這情景。台灣,也不是一個黨國了。無論怎樣,1911年10月10日這個日子,也是值得大家紀念,那是國父孫中山先山發起武昌起義的日子。

Ubunutu 10.10 將於10/10/10推出。
不知道 Ubuntu 是甚麼?這是一個 Linux 作業系統。是現今 Desktop Computer 上,最多人使用的一個 Linux distribution。當然,Desktop OS 市場上,最多人使用的是 Windows。MacOSX + Linux,市場佔有率合共不足 10% 。我第一次安裝 Linux,已是十年前的事了,那是 Ubuntu 還未出現。不過係近兩三年先至認真去使用 linux,是用 ubuntu 系列呢。今年年初,甚至把 windows 剷掉了,只行 Ubuntu。用了 Ubuntu 三年,真係好用、易用。Package Management 真是一個好東西,反而要付費的 Windows 竟然沒有 Package Management 。
近一星期,我轉用了 Arch Linux。不是 Ubuntu 有甚麼特別問題,初次使用 Linux 的人士,我是極力建議用 Ubuntu 的。只是我有些認同 Arch Linux 的理念,於是便試試。
記得 Ubuntu 9.10 升級至 10.04,感覺上作業系統的效能提升了不少,一反近年 OS 越來越大食的傳統。希望 Ubuntu 10.10 更上一層樓。
有無覺得奇怪,Ubuntu 這一代的 version number 是10.10,結合推出的日子,豈不是1010101010?沒有用過 Ubuntu 的人可能會覺得很神奇。Ubuntu 習慣上每半年進行一次大規模的更新,分別在每年的4月和10月,而它的 version number 是和推出日子有關。例如 Ubuntu 8.04,就是08年4月推出的版本,9.10是09年10月推出的版本,如此類推。接著會在10年10月推出新版本,當然就是 version 10.10了。
Answer to the Ultimate Question of Life, the Universe and Everything
其實 Ubuntu 通常會在月底推出新版本,今次為何會選10月10日?中文字就有「十全十美」,外國又有甚麼意義?
據高層人士 Mark Shuttleworth 的解釋就是把101010看作二進制數,轉為10進制數便是42,而42就是 answer to the ultimate question of life, the universe and everything。
一頭霧水?這是外國一本著明科幻搞笑小說,The Hitchhiker's Guide to Galaxy 的其中一個橋段。
詳情請看:
http://en.wikipedia.org/wiki/Phrases_from_The_Hitchhiker%27s_Guide_to_the_Galaxy
http://en.wikipedia.org/wiki/The_Hitchhiker%27s_Guide_to_the_Galaxy
這部小說亦曾拍成電影,也曾在香港上畫,當時譯作「星際快閃黨」。當年阿伯拉左我去睇,是一套幾好看的 Cult Film。不過可能香港唔太收得,我地要去到一間很 up dup 的戲院,入面一陣發霉的氣味……
套戲幾搞笑,不過中文字幕太爛……我曾經想找番 DVD 來看,但找了幾間店舖也找不到。
10/10/10這個日子,撞正是星期日,加上宜嫁娶,很多新人也選擇在這天拉埋天窗。酒席預早年多前預訂也爆滿。
祝所有無論是否在10年10月10日結婚的男男女女,也可以和另一半共度一個幸福人生。
10/10/10,中華民國建國九十九週年,首次出現「三十節」。(惡搞,速逃,哈哈哈~~~)
以前臨近雙十節,香港都有不少地方會掛起青天白日旗。現今香港回歸後,當然不會有這情景。台灣,也不是一個黨國了。無論怎樣,1911年10月10日這個日子,也是值得大家紀念,那是國父孫中山先山發起武昌起義的日子。

Ubunutu 10.10 將於10/10/10推出。
不知道 Ubuntu 是甚麼?這是一個 Linux 作業系統。是現今 Desktop Computer 上,最多人使用的一個 Linux distribution。當然,Desktop OS 市場上,最多人使用的是 Windows。MacOSX + Linux,市場佔有率合共不足 10% 。我第一次安裝 Linux,已是十年前的事了,那是 Ubuntu 還未出現。不過係近兩三年先至認真去使用 linux,是用 ubuntu 系列呢。今年年初,甚至把 windows 剷掉了,只行 Ubuntu。用了 Ubuntu 三年,真係好用、易用。Package Management 真是一個好東西,反而要付費的 Windows 竟然沒有 Package Management 。
近一星期,我轉用了 Arch Linux。不是 Ubuntu 有甚麼特別問題,初次使用 Linux 的人士,我是極力建議用 Ubuntu 的。只是我有些認同 Arch Linux 的理念,於是便試試。
Simplicity is the ultimate sophistication.
by Leonardo Da Vinci
by Leonardo Da Vinci
記得 Ubuntu 9.10 升級至 10.04,感覺上作業系統的效能提升了不少,一反近年 OS 越來越大食的傳統。希望 Ubuntu 10.10 更上一層樓。
有無覺得奇怪,Ubuntu 這一代的 version number 是10.10,結合推出的日子,豈不是1010101010?沒有用過 Ubuntu 的人可能會覺得很神奇。Ubuntu 習慣上每半年進行一次大規模的更新,分別在每年的4月和10月,而它的 version number 是和推出日子有關。例如 Ubuntu 8.04,就是08年4月推出的版本,9.10是09年10月推出的版本,如此類推。接著會在10年10月推出新版本,當然就是 version 10.10了。
Answer to the Ultimate Question of Life, the Universe and Everything
其實 Ubuntu 通常會在月底推出新版本,今次為何會選10月10日?中文字就有「十全十美」,外國又有甚麼意義?
據高層人士 Mark Shuttleworth 的解釋就是把101010看作二進制數,轉為10進制數便是42,而42就是 answer to the ultimate question of life, the universe and everything。
一頭霧水?這是外國一本著明科幻搞笑小說,The Hitchhiker's Guide to Galaxy 的其中一個橋段。
詳情請看:
http://en.wikipedia.org/wiki/Phrases_from_The_Hitchhiker%27s_Guide_to_the_Galaxy
http://en.wikipedia.org/wiki/The_Hitchhiker%27s_Guide_to_the_Galaxy
這部小說亦曾拍成電影,也曾在香港上畫,當時譯作「星際快閃黨」。當年阿伯拉左我去睇,是一套幾好看的 Cult Film。不過可能香港唔太收得,我地要去到一間很 up dup 的戲院,入面一陣發霉的氣味……
套戲幾搞笑,不過中文字幕太爛……我曾經想找番 DVD 來看,但找了幾間店舖也找不到。
10/10/10這個日子,撞正是星期日,加上宜嫁娶,很多新人也選擇在這天拉埋天窗。酒席預早年多前預訂也爆滿。
祝所有無論是否在10年10月10日結婚的男男女女,也可以和另一半共度一個幸福人生。
Sunday, August 22, 2010
Pigeonhole Principle
Pigeonhole Principle,中譯鴿籠原理。簡單來說,把 n 隻鴿子分配到 m 個鴿籠中,若 n > m,則最少有一個鴿籠內有多於一隻鴿子。
很多 sources 也是引述這個版本,不過死肥仔其實是有個惡搞版:
把 n 隻鴿子分配到 m 個鴿籠中,若 n > m,一係會有鴿子無籠住,一係有些鴿子會迫埋在同一個籠內,哈哈哈哈))))
另外,還有一個較數學的描述,是用到 mapping (映射)。詳見 wikipedia:
點解突然提起這東西?我也不知道點解,只是突然想起來,便懷念一下舊事。
你們知道我在甚麼情況下第一次聽見「鴿籠原理」四個大字嗎?是均爺!
當時的情形還有些少印象。話說十幾年前,一班朋友在討論一道 IQ 題,突然,有人解破了題目,並把答案說出來。這時候,均爺一副世外高人的口吻彈出:「鴿籠原理」。
我覺得「鴿籠原理」這個名稱很 cool 呀!立即追問究竟那是甚麼,均爺就再向我們解釋。
那應該是入大學前的事,但究竟是甚麼 IQ 題,解破的仁兄是誰,我已忘記了,只記得均爺一句:「鴿籠原理」。你們有誰記得呢?記得的話留個言吧。
均爺真係時有金句。唔知你的單車之旅如何,個旅程 blog 很久沒有更新了,不會是有甚麼阻滯吧。
大家覺得這定理容易理解嗎?我覺得是少數一講就明的數學定理。不過我曾經用鴿籠原理向人解釋在十三人內必定會有些人在同一個月份生日,那人好像一頭霧水……是我表達能力太差吧。
還有一些幾搞笑的應用,例如在香港必定找到最少兩人有相同數目的頭髮。把香港人數當作鴿子,即700萬隻鴿子,頭髮數目當在鴿籠,很明顯頭髮數目遠遠少於700萬,因此必會有些人有相同數目的頭髮。
我還見過一個例子,幾特別,我真係無想過可以應用到鴿籠原理:
用兩枝不同顏色的筆填滿一張A4白紙,你必定能在紙上找出兩點相距1cm,且兩點顏色不同。
解法如下:
在紙上畫一個邊長1cm的等邊三角形(位置無乜所謂),把兩種顏色看作是鴿籠,三角形的三個頂點看作是鴿子……看很出來吧?
我覺得這個解法確實精妙。
Tuesday, May 25, 2010
夢
很恐怖,昨晚發了一個夢,一個關於數學的夢,訓醒後比平日更加累。
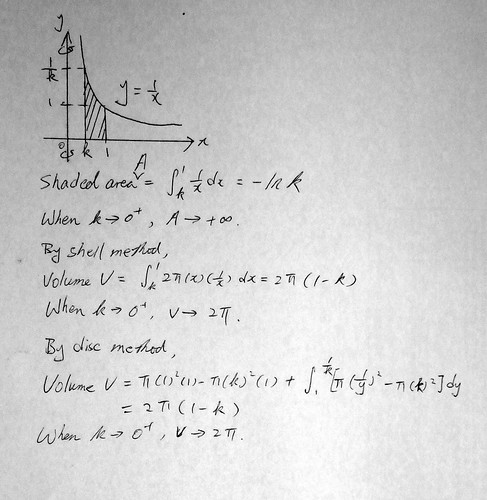
不是甚麼高深數學,或許大家以前也有想過。不過我應該沒有想過,或者想過都忘記了,但竟然在夢中出現……點解唔係發夢見到下期六合彩號碼呢……在夢中,我考慮曲線 y=1/x (其中x>0)。我在計算一個旋轉體的體積,該旋轉體是由曲線y=1/x、直線 x=k(其中 0< k <1)、x=1 和 x 軸所圍成的區域繞著 y 軸旋轉360度所形成。
在夢中,我用shell method,很快計到該立體的體積是 2*Pi*(1-k)。
當時令我驚訝的,是當 k 趨向 0 時,該體積會趨向 2*Pi!不神奇嗎?該曲線在 x 趨向 0 的時候 y 的值是無界的,該區域在 k 趨向 0 時候面積也是無界的!但那個立體的體積竟然是一個特定的值!我感到十分惆悵。
上班途中在巴士上試下用disc method 來計算一下,當然也得出相同的結果。
其實類似的結果,在幾何級數 ( geometric series) 中常會出現,例如著明的 Koch snowflake,便是一個周界無限但面積有限的平面圖形。
這些吊詭的結果,是因為我們感觀上的面積和體積,與數學中的面積和體積是有分別吧?不過我依然感到惆悵……
wikipeidia 上關於 Koch snowflake 的介紹:
http://en.wikipedia.org/wiki/Koch_snowflake
********************************************************
********************************************************
近日實在很累,欠下很多 blog 債。
有些長篇大論的,唔想打……或者打打下未完成,實在很費神,例如對電影 ironman2、猛鬼街的感想、對516的感想、一些對初等數學、數學教育的看法……
就算短短地的,也沒有精力去完成。
隨著時間的流逝,一切也淡忘……
不是甚麼高深數學,或許大家以前也有想過。不過我應該沒有想過,或者想過都忘記了,但竟然在夢中出現……點解唔係發夢見到下期六合彩號碼呢……在夢中,我考慮曲線 y=1/x (其中x>0)。我在計算一個旋轉體的體積,該旋轉體是由曲線y=1/x、直線 x=k(其中 0< k <1)、x=1 和 x 軸所圍成的區域繞著 y 軸旋轉360度所形成。
在夢中,我用shell method,很快計到該立體的體積是 2*Pi*(1-k)。
當時令我驚訝的,是當 k 趨向 0 時,該體積會趨向 2*Pi!不神奇嗎?該曲線在 x 趨向 0 的時候 y 的值是無界的,該區域在 k 趨向 0 時候面積也是無界的!但那個立體的體積竟然是一個特定的值!我感到十分惆悵。
上班途中在巴士上試下用disc method 來計算一下,當然也得出相同的結果。
其實類似的結果,在幾何級數 ( geometric series) 中常會出現,例如著明的 Koch snowflake,便是一個周界無限但面積有限的平面圖形。
這些吊詭的結果,是因為我們感觀上的面積和體積,與數學中的面積和體積是有分別吧?不過我依然感到惆悵……

wikipeidia 上關於 Koch snowflake 的介紹:
http://en.wikipedia.org/wiki/Koch_snowflake
********************************************************
********************************************************
近日實在很累,欠下很多 blog 債。
有些長篇大論的,唔想打……或者打打下未完成,實在很費神,例如對電影 ironman2、猛鬼街的感想、對516的感想、一些對初等數學、數學教育的看法……
就算短短地的,也沒有精力去完成。
隨著時間的流逝,一切也淡忘……
Tuesday, March 16, 2010
Cross Product
以前讀過一些文章,知道近年隨著三維遊戲的流行,為了提供更快的三維圖像處理能力,新型的圖像處理器 (GPU)都在硬件上直接支援計算 matrix , vector 等功能,其中一個功能,就是 Cross Product。
最近不知痴了邊條筋,發覺原來 2x2 system of linear equations 的解,其實可以用 Cross Product 來表示。
(說穿了其實很簡單,但點解我十幾年來的都無這樣想過呢 >.< )
考慮二元一次方程組:
[[a1, b1], [a2, b2]]*[[x], [y]] = [[c1], [c2]]
(希望你們看得明我打乜,因為我懶畫出來……)
利用Cramer's Rule,我們可得出 x=P/R, y=Q/R 這一組解,其中P、Q和R 是三個determinants :
P=det([c1, b1], [c2, b2])
Q=det([a1, c1], [a2, c2])
R=det([a1, b1], [a2, b2])
另一方面考慮向量g和h:
g=(a1)i+(b1)j+(c1)k
h=(a2)i+(b2)j+(c2)k
利用 rule of Sarrus,
g x h ( 即是 cross product of g and h)
=det([i, j, k], [a1, b1, c1], [a2, b2, c2])
=det([b1, c1], [b2, c2])i - det([a1, c1], [a2, c2])j + det([a1, b1], [a2, b2])k
=-det([c1, b1], [c2, b2])i - det([a1, c1], [a2, c2])j + det([a1, b1], [a2, b2])k
=-Pi - Qj + Rk
看到嗎?再次出現 P、Q和R,這就是方程組的解與 cross product 的關係。
GPU 在硬件上支援 cross product 的計算,即是代表著輸入 a1, a2, b1, b2, c1, c2,便可直接得出 P、Q和R的值。
傳統數學、計算機運算上,要從a1, a2, b1, b2, c1, c2,得出 P、Q和R的值,須計算 determinants,即是要計算數個加減乘除的運算。
看來利用 GPU 的 Cross product 計算功能能,能更有效地解二元一次方程組吧?
不知到 GPU 的 instruction set 上還包括甚麼運算呢?利用這些運算,或許可以得出很多一反傳統的高效能計算法則吧。
最近不知痴了邊條筋,發覺原來 2x2 system of linear equations 的解,其實可以用 Cross Product 來表示。
(說穿了其實很簡單,但點解我十幾年來的都無這樣想過呢 >.< )
考慮二元一次方程組:
[[a1, b1], [a2, b2]]*[[x], [y]] = [[c1], [c2]]
(希望你們看得明我打乜,因為我懶畫出來……)
利用Cramer's Rule,我們可得出 x=P/R, y=Q/R 這一組解,其中P、Q和R 是三個determinants :
P=det([c1, b1], [c2, b2])
Q=det([a1, c1], [a2, c2])
R=det([a1, b1], [a2, b2])
另一方面考慮向量g和h:
g=(a1)i+(b1)j+(c1)k
h=(a2)i+(b2)j+(c2)k
利用 rule of Sarrus,
g x h ( 即是 cross product of g and h)
=det([i, j, k], [a1, b1, c1], [a2, b2, c2])
=det([b1, c1], [b2, c2])i - det([a1, c1], [a2, c2])j + det([a1, b1], [a2, b2])k
=-det([c1, b1], [c2, b2])i - det([a1, c1], [a2, c2])j + det([a1, b1], [a2, b2])k
=-Pi - Qj + Rk
看到嗎?再次出現 P、Q和R,這就是方程組的解與 cross product 的關係。
GPU 在硬件上支援 cross product 的計算,即是代表著輸入 a1, a2, b1, b2, c1, c2,便可直接得出 P、Q和R的值。
傳統數學、計算機運算上,要從a1, a2, b1, b2, c1, c2,得出 P、Q和R的值,須計算 determinants,即是要計算數個加減乘除的運算。
看來利用 GPU 的 Cross product 計算功能能,能更有效地解二元一次方程組吧?
不知到 GPU 的 instruction set 上還包括甚麼運算呢?利用這些運算,或許可以得出很多一反傳統的高效能計算法則吧。
Monday, January 11, 2010
統計的應用和誤用
不知大家還記得在中學的數學堂上,曾學個一個名為「統計的應用和誤用」的課題嗎?
內裏其中有部分內容,是向同學指出現實生活中有些媒體利用統計學來扮專業誤導大家。例如統計圖上的坐標軸沒有清楚列出比例,甚至不按比例。又例如問卷內的問題計設極具誤導性份,像是:大量使用膠袋是破壞環境的行為,你認為超級市場應該停止免費派發膠袋嗎?
早兩日,朋友 send 了一條 link 給我看。
http://blog.tiney.com/?p=5446
這是某位仁兄的 blog,談及「智經」關於高鐵的問卷條查。我一看,實在為之一震。
以前我心想,連中學生都看得穿的用統計誤導手法,應該不會有人中招,現實中應該無乜人夠膽去用。但實情並非如此。那仁兄羅列了當中的一些問題,簡直全是中學課本來所提及的誤導手法,直情可以100%照單全收放入課本做事例。(不知道課本送審時班官見到這個事例會否作出留難 XDDDDDD)
現實就係咁弱智。那個甚麼機構呀?班大學統計教授死屎架?
或者由另一個角度去想,原來中學生的統計知識已足以在大學內呃飯食。
學習這課題,重點不是去不被誤導,而是怎樣用來誤導別人,哈哈哈)))
不過諗落,怎去避免不受誤導?
作為受訪者,如果識破被誤導,又如可?可以告佢嗎?大不了爆粗鬧佢幾句然後收線。那機構也只是當這個回應不存在吧。
作為報刊的讀者,就更無耐。看到報章知道原來大部分人也讚成起高鐵,又如何?最多心想,正合我意/不合我意。報刊大多不會詳述調查手法,問卷設計等資料,只會報導結果,最多請幾個學者狗UP兩句,咁就搞掂。
哈哈哈,以後唔好話中學數學無鬼用~~~
內裏其中有部分內容,是向同學指出現實生活中有些媒體利用統計學來扮專業誤導大家。例如統計圖上的坐標軸沒有清楚列出比例,甚至不按比例。又例如問卷內的問題計設極具誤導性份,像是:大量使用膠袋是破壞環境的行為,你認為超級市場應該停止免費派發膠袋嗎?
早兩日,朋友 send 了一條 link 給我看。
http://blog.tiney.com/?p=5446
這是某位仁兄的 blog,談及「智經」關於高鐵的問卷條查。我一看,實在為之一震。
以前我心想,連中學生都看得穿的用統計誤導手法,應該不會有人中招,現實中應該無乜人夠膽去用。但實情並非如此。那仁兄羅列了當中的一些問題,簡直全是中學課本來所提及的誤導手法,直情可以100%照單全收放入課本做事例。(不知道課本送審時班官見到這個事例會否作出留難 XDDDDDD)
現實就係咁弱智。那個甚麼機構呀?班大學統計教授死屎架?
或者由另一個角度去想,原來中學生的統計知識已足以在大學內呃飯食。
學習這課題,重點不是去不被誤導,而是怎樣用來誤導別人,哈哈哈)))
不過諗落,怎去避免不受誤導?
作為受訪者,如果識破被誤導,又如可?可以告佢嗎?大不了爆粗鬧佢幾句然後收線。那機構也只是當這個回應不存在吧。
作為報刊的讀者,就更無耐。看到報章知道原來大部分人也讚成起高鐵,又如何?最多心想,正合我意/不合我意。報刊大多不會詳述調查手法,問卷設計等資料,只會報導結果,最多請幾個學者狗UP兩句,咁就搞掂。
哈哈哈,以後唔好話中學數學無鬼用~~~
Wednesday, January 06, 2010
誤差
早前幫同事去買刷膠,用我的會員卡有九折優惠。
一塊刷膠售 $2.5,九折後售價是多少?$2.25?你錯了,沒有豆零了,須四捨五入至最接近的 $0.1,即是 $2.3。
但我購買了6塊,付款前我作出如下計算 $2.5 * 6 * 0.9 = $13.5。
近乎不可能發生的時情竟然會發生,如此簡單的小學數,我竟然計錯了!收銀機顯示我應付 $13.8,我立時愣一愣。
隨即我意會到,原來收銀機盤數是這樣計算的:
$2.5 * 0.9 = $2.25
捨入至 $2.3
$2.3 * 6 = $13.8
立時,我有一種被搵笨的感覺!
為甚麼不是全單作九折再四捨五入 (下稱方法A),而是逐個項目先來九折,繼而四捨五入,最後才加總(下稱方法B)?
用方法A,全單的最大絕對誤差是 $0.05。
但用方法B呢?最大絕對誤差是無上限的。例如在以上我購買刷膠的例子中,全單的最大絕對誤差是$0.3!如果我購買600塊刷膠,最大絕對誤差便會是$30!
當然,無論用方法A還是方法B,捨入時採用四捨五入,而不是單單的上捨入或下捨入,那個誤差便會有可能是正數,亦有可能是負數。即是說顧客有機會被「搵笨」,也有機會拿「著數」。不過人就係咁犯賤,拿到「著數」可不會太上心呢,哈哈哈)))))))))))
對店舖來說,如果價錢的毫子位分佈平均,無論用方法A還是方法B,長遠來計這個誤差應該正負相抵,最終接近0。
那為甚麼要用方法B,而不用方法A呢?在我的角度,我覺得方法A實在直接得多!想了一會,會是以下原因嗎?
首先,價錢的毫子位,分佈實在不是平均!大多數店舖,價錢不是整數,如$13, $20, $100,便是五毫,如$2.5, $33.5。
這有甚麼問題?以九折來計,整數的取九折後,是不用再作捨入的。但五毫呢?必會是上捨入,例如
$2.5 * 0.9 = $2.25 ~~ $2.3
$33.5 * 0.9 = $30.15 ~~ $30.2
看到嗎?即是說顧客被「搵笨」了。
不從這個屎檜的角度想,會有其他原因嗎?
我猜測是方便電腦作記錄吧。
如果系統要記錄每件售出的貨品的售價,用方法B應該較簡單。
例如以$2.5的刷膠為例,系統只須記錄正價出售的 $2.5,以及九折出售的 $2.3。
但用方法A呢?便有正價的 $2.5,九折後有以下情況:
同一張單售出一件的話,折扣後每件售價是 $2.3。
同一張單售出兩件的話,折扣後是 $2.5 * 2 * 0.9 = $4.5,這個 $4.5 是顧客所付的,不用捨入,但電腦作記錄要記錄每件售出的金額的話,便是 $4.5/2 = $2.25
即是說同一件物品,會出現多於一個單位售價。
我對銷售系統沒有去研究,但從上例所見,採用方法A會有較多問題須作考慮。
*********************************************************************
想呀想,其實我還想過一件無聊事。如果物品售 $0.5,九折後是 $0.45,四捨五入後是 $0.5,那麼便沒有折扣嗎?
採用方法 B 的話,我就算買 100 件 $0.5 的貨品也不會享有九折優惠嗎?這可算一個極端例子呢,哈哈哈)))))))))))
可惜店舖內找不到價值 $0.5 的貨品,未能去驗證。
一塊刷膠售 $2.5,九折後售價是多少?$2.25?你錯了,沒有豆零了,須四捨五入至最接近的 $0.1,即是 $2.3。
但我購買了6塊,付款前我作出如下計算 $2.5 * 6 * 0.9 = $13.5。
近乎不可能發生的時情竟然會發生,如此簡單的小學數,我竟然計錯了!收銀機顯示我應付 $13.8,我立時愣一愣。
隨即我意會到,原來收銀機盤數是這樣計算的:
$2.5 * 0.9 = $2.25
捨入至 $2.3
$2.3 * 6 = $13.8
立時,我有一種被搵笨的感覺!
為甚麼不是全單作九折再四捨五入 (下稱方法A),而是逐個項目先來九折,繼而四捨五入,最後才加總(下稱方法B)?
用方法A,全單的最大絕對誤差是 $0.05。
但用方法B呢?最大絕對誤差是無上限的。例如在以上我購買刷膠的例子中,全單的最大絕對誤差是$0.3!如果我購買600塊刷膠,最大絕對誤差便會是$30!
當然,無論用方法A還是方法B,捨入時採用四捨五入,而不是單單的上捨入或下捨入,那個誤差便會有可能是正數,亦有可能是負數。即是說顧客有機會被「搵笨」,也有機會拿「著數」。不過人就係咁犯賤,拿到「著數」可不會太上心呢,哈哈哈)))))))))))
對店舖來說,如果價錢的毫子位分佈平均,無論用方法A還是方法B,長遠來計這個誤差應該正負相抵,最終接近0。
那為甚麼要用方法B,而不用方法A呢?在我的角度,我覺得方法A實在直接得多!想了一會,會是以下原因嗎?
首先,價錢的毫子位,分佈實在不是平均!大多數店舖,價錢不是整數,如$13, $20, $100,便是五毫,如$2.5, $33.5。
這有甚麼問題?以九折來計,整數的取九折後,是不用再作捨入的。但五毫呢?必會是上捨入,例如
$2.5 * 0.9 = $2.25 ~~ $2.3
$33.5 * 0.9 = $30.15 ~~ $30.2
看到嗎?即是說顧客被「搵笨」了。
不從這個屎檜的角度想,會有其他原因嗎?
我猜測是方便電腦作記錄吧。
如果系統要記錄每件售出的貨品的售價,用方法B應該較簡單。
例如以$2.5的刷膠為例,系統只須記錄正價出售的 $2.5,以及九折出售的 $2.3。
但用方法A呢?便有正價的 $2.5,九折後有以下情況:
同一張單售出一件的話,折扣後每件售價是 $2.3。
同一張單售出兩件的話,折扣後是 $2.5 * 2 * 0.9 = $4.5,這個 $4.5 是顧客所付的,不用捨入,但電腦作記錄要記錄每件售出的金額的話,便是 $4.5/2 = $2.25
即是說同一件物品,會出現多於一個單位售價。
我對銷售系統沒有去研究,但從上例所見,採用方法A會有較多問題須作考慮。
*********************************************************************
想呀想,其實我還想過一件無聊事。如果物品售 $0.5,九折後是 $0.45,四捨五入後是 $0.5,那麼便沒有折扣嗎?
採用方法 B 的話,我就算買 100 件 $0.5 的貨品也不會享有九折優惠嗎?這可算一個極端例子呢,哈哈哈)))))))))))
可惜店舖內找不到價值 $0.5 的貨品,未能去驗證。
Monday, October 26, 2009
複數的出現
大家還記得學習複數 (complex number) 時,書本上是怎樣引入的呢?
通常是:
數學家在研究三次方程 (cubic equation) 的求根公式時,發現了複數……
又或者
為了使 x^2 = -1, x^2 = -2......等方程有解,於是引入 i = sqrt(-1)
輕輕地交代了複數的發現,然後,大家便利用 i^2 = -1 這規則,再加上一直以來在實數四則運算見慣的交換律、分配律,進行複數的運算。
我想大約在我讀預科時,我「相信」複數是由數學家研究三次方程時開始被重視,因為我見過很多書都係咁講。而「為了使 x^2=-1, x^2=-2......等方程有解,於是引入 i=sqrt(-1)」只是一些書本簡便起見作出的引子吧。
那是我只是信,相信權威吧,但沒有其他理性上的理據說服到我。
當時我心入面有幾個問題:
1. 為甚麼要把 a+bi 看作「複數」,單單處理「bi」不行嗎?隨著接觸數學越來越多,我知道以「a+bi」作一個整體來看待,會引發出往後數學上很多豐盛的成果。
2. 為甚麼是在求「三次」方程才開以注意到複數?其實在二次方程的求根公式,有時都需要處理開方根號內帶有負數的問題 (即二次方程的判別式 b^2 - 4ac < 0)。
到近年 (近兩三年吧,近兩三年無乜時間觀念,忘了是何時了),我才想出一個令我接受的原因。
(這個純粹是我令自己接受的原因,未必是正確的原因,我也沒有去考究現今主流研究數學史的學者是否抱著這觀點。)
先看二次方程的情況。我們可把二次方程 ax^2 + bx + c =0 寫成
x^2 - mx - n = 0, 其中 m = -(b/a), n = -(c/a)
移項得出
x^2 = mx + n
好戲在後頭,引入未知數 y,得出以下聯立方程:
y = x^2 及 y = mx + n
原來的二次方程的根,便是這個方程組中 x 的解了。點解我要咁做?我想在直角坐標平面上「看」二次方程的解。
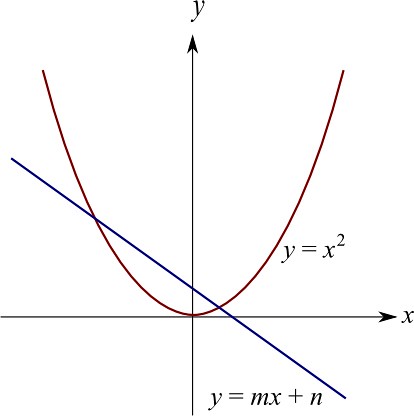
圖中顯示出 y = x^2 與 y = mx + n 的圖像。交點的 x 坐標便是原本二次方程的解。
不難想像,不同的 m 和 n 的值,就可代表不同的二次方程。
圖像中,y=x^2 這拋物線不變,改變直線 (即 m 和 n 的值),就可代表了不同的二次方程。大家有否發現,不是所有直線都與拋物線有交點?例如把我的附圖中的直線往下移,便會得出一條與拋物線不相交的直線。
沒有交點,即是方程無解吧!也就是判別式 b^2 - 4ac < 0。
因此,在解二次方程時,若 b^2 - 4ac < 0,我們可以不去深究 sqrt(b^2 - 4ac) 究竟是甚麼。無解就是無解啦,無交點就是無交點啦,不存在就是不存在啦,何須自找麻煩去研究這些不存在的東西?
真的不用理嗎?看看三次方程的情況。
三次方程 x^3 + ax^2 + bx + c = 0,可以變換為
t^3 + pt + q = 0 (設 t = x - a/3 )
與二次方程的做法相似,改寫成
y = t^3 及 y = - pt - q
這樣便可在 yt 平面上觀察解的情況。
下圖是 y = t^3 的圖像:

這三次函數的圖像,與二次函數 y = x^2 的圖像有一個很明顯的分別,就是沒有最低點。
給定任意一個 y 值,我們都可以找到圖像上對應的 t 值。當在圖上加上直線,必定會與曲線相交!這代表著三次方程「必定」有解。
但看看三次方程 t^3 + pt + q = 0 的求根公式:
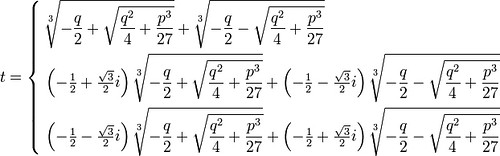
這公式我是在 wiki 抓下來,三個公式中,都有 sqrt((q^2)/4 + (p^3)/27) 這項。
設 q = 0, p=3,代入第一個公式,我們得出 t = 0 是一個解,是方程 t^3 + 3t = 0 的一個解。這個解與我們用因式分解得出的結果是一致的!
就係咁簡單?還未完。
看看方程 t^3 - 57t + 56 = 0,大家可把 t = -8, 1, 7 代入方程,發現它們是該方程的根。
繪畫 y = t^3 與 y = 57t - 56 的圖像,它們會於 t = -8, 1, 7 三處相交!
但是,把 p = -57 及 q = 56 代入求根公式,
會發現 (q^2)/4 + (p^3)/27 = -6075,即 sqrt((q^2)/4 + (p^3)/27) = sqrt(-6075) 不是實數
在第一個公式會得出
(-28 + sqrt(-6075))^(1/3) + (-28 - sqrt(-6075))^(1/3)
注意在第一個公式中,本身沒有複數。但我們看到要利用這公式求得這方程的解(實數),我們先要懂得處理負數的開方根及有關的運算,即是複數的運算!(以上式子的結果為 7)
二次方程中,若 b^2 - 4ac < 0,公式涉及 sqrt(負數),我們說方程無解,結果與圖像無交點是一致的。
而三次方程中,若 (q^2)/4 + (p^3)/27 < 0,公式涉及 sqrt(負數),但我們不能就此指出方程無解,這會與圖像有交點的程況不一致!
這次,我們無得再逃避了,要達到求三次方程的根這個目標,必先要好好研究這類「新」的數的運算!
就是這個圖像上的原因,令我接受書本上所謂由解三次方程開始才重視複數的事實。
這原因是對?是錯?我不知。很大程度取決於當時數學家怎樣看方程的圖像這概念。事實上,坐標幾何的出現,現今歸功於十七世紀笛卡兒 (Rene Descartes, 1596 - 1650) 的貢獻,這是在三次方程求根公式之後發生的事情。不過數學發展不是石頭爆出來的,之前都有很多痕跡可尋。例如遠在古希臘的阿波羅尼奧斯 (Apollonius, 262BC - 196 BC),他處理圓錐曲線的一些技巧與現今坐標幾何的方法相近。所以我覺得15、16 世紀數學家是從圖像令他們不重視二次方程的複數解,但在三次方程時要認真處理,也不足為奇。
世事就是咁神奇,以為可以避開,當佢不存在便何。實際上,不存在真的不存在嗎?避無可避,終於要面對。
避到就是好,避唔到就是禍?未必如此。
終於發現了複數。但往後的發展十分緩慢,一直要過多兩三百年,Gauss、Argand 等人給出「複平面」,發展開始快得多,再由黎曼推上一個頂峰。
通常是:
數學家在研究三次方程 (cubic equation) 的求根公式時,發現了複數……
又或者
為了使 x^2 = -1, x^2 = -2......等方程有解,於是引入 i = sqrt(-1)
輕輕地交代了複數的發現,然後,大家便利用 i^2 = -1 這規則,再加上一直以來在實數四則運算見慣的交換律、分配律,進行複數的運算。
我想大約在我讀預科時,我「相信」複數是由數學家研究三次方程時開始被重視,因為我見過很多書都係咁講。而「為了使 x^2=-1, x^2=-2......等方程有解,於是引入 i=sqrt(-1)」只是一些書本簡便起見作出的引子吧。
那是我只是信,相信權威吧,但沒有其他理性上的理據說服到我。
當時我心入面有幾個問題:
1. 為甚麼要把 a+bi 看作「複數」,單單處理「bi」不行嗎?隨著接觸數學越來越多,我知道以「a+bi」作一個整體來看待,會引發出往後數學上很多豐盛的成果。
2. 為甚麼是在求「三次」方程才開以注意到複數?其實在二次方程的求根公式,有時都需要處理開方根號內帶有負數的問題 (即二次方程的判別式 b^2 - 4ac < 0)。
到近年 (近兩三年吧,近兩三年無乜時間觀念,忘了是何時了),我才想出一個令我接受的原因。
(這個純粹是我令自己接受的原因,未必是正確的原因,我也沒有去考究現今主流研究數學史的學者是否抱著這觀點。)
先看二次方程的情況。我們可把二次方程 ax^2 + bx + c =0 寫成
x^2 - mx - n = 0, 其中 m = -(b/a), n = -(c/a)
移項得出
x^2 = mx + n
好戲在後頭,引入未知數 y,得出以下聯立方程:
y = x^2 及 y = mx + n
原來的二次方程的根,便是這個方程組中 x 的解了。點解我要咁做?我想在直角坐標平面上「看」二次方程的解。

圖中顯示出 y = x^2 與 y = mx + n 的圖像。交點的 x 坐標便是原本二次方程的解。
不難想像,不同的 m 和 n 的值,就可代表不同的二次方程。
圖像中,y=x^2 這拋物線不變,改變直線 (即 m 和 n 的值),就可代表了不同的二次方程。大家有否發現,不是所有直線都與拋物線有交點?例如把我的附圖中的直線往下移,便會得出一條與拋物線不相交的直線。
沒有交點,即是方程無解吧!也就是判別式 b^2 - 4ac < 0。
因此,在解二次方程時,若 b^2 - 4ac < 0,我們可以不去深究 sqrt(b^2 - 4ac) 究竟是甚麼。無解就是無解啦,無交點就是無交點啦,不存在就是不存在啦,何須自找麻煩去研究這些不存在的東西?
真的不用理嗎?看看三次方程的情況。
三次方程 x^3 + ax^2 + bx + c = 0,可以變換為
t^3 + pt + q = 0 (設 t = x - a/3 )
與二次方程的做法相似,改寫成
y = t^3 及 y = - pt - q
這樣便可在 yt 平面上觀察解的情況。
下圖是 y = t^3 的圖像:

這三次函數的圖像,與二次函數 y = x^2 的圖像有一個很明顯的分別,就是沒有最低點。
給定任意一個 y 值,我們都可以找到圖像上對應的 t 值。當在圖上加上直線,必定會與曲線相交!這代表著三次方程「必定」有解。
但看看三次方程 t^3 + pt + q = 0 的求根公式:
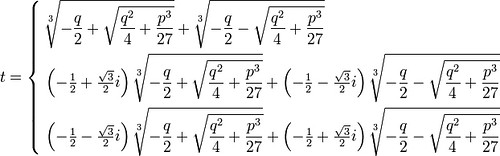
這公式我是在 wiki 抓下來,三個公式中,都有 sqrt((q^2)/4 + (p^3)/27) 這項。
設 q = 0, p=3,代入第一個公式,我們得出 t = 0 是一個解,是方程 t^3 + 3t = 0 的一個解。這個解與我們用因式分解得出的結果是一致的!
就係咁簡單?還未完。
看看方程 t^3 - 57t + 56 = 0,大家可把 t = -8, 1, 7 代入方程,發現它們是該方程的根。
繪畫 y = t^3 與 y = 57t - 56 的圖像,它們會於 t = -8, 1, 7 三處相交!
但是,把 p = -57 及 q = 56 代入求根公式,
會發現 (q^2)/4 + (p^3)/27 = -6075,即 sqrt((q^2)/4 + (p^3)/27) = sqrt(-6075) 不是實數
在第一個公式會得出
(-28 + sqrt(-6075))^(1/3) + (-28 - sqrt(-6075))^(1/3)
注意在第一個公式中,本身沒有複數。但我們看到要利用這公式求得這方程的解(實數),我們先要懂得處理負數的開方根及有關的運算,即是複數的運算!(以上式子的結果為 7)
二次方程中,若 b^2 - 4ac < 0,公式涉及 sqrt(負數),我們說方程無解,結果與圖像無交點是一致的。
而三次方程中,若 (q^2)/4 + (p^3)/27 < 0,公式涉及 sqrt(負數),但我們不能就此指出方程無解,這會與圖像有交點的程況不一致!
這次,我們無得再逃避了,要達到求三次方程的根這個目標,必先要好好研究這類「新」的數的運算!
就是這個圖像上的原因,令我接受書本上所謂由解三次方程開始才重視複數的事實。
這原因是對?是錯?我不知。很大程度取決於當時數學家怎樣看方程的圖像這概念。事實上,坐標幾何的出現,現今歸功於十七世紀笛卡兒 (Rene Descartes, 1596 - 1650) 的貢獻,這是在三次方程求根公式之後發生的事情。不過數學發展不是石頭爆出來的,之前都有很多痕跡可尋。例如遠在古希臘的阿波羅尼奧斯 (Apollonius, 262BC - 196 BC),他處理圓錐曲線的一些技巧與現今坐標幾何的方法相近。所以我覺得15、16 世紀數學家是從圖像令他們不重視二次方程的複數解,但在三次方程時要認真處理,也不足為奇。
世事就是咁神奇,以為可以避開,當佢不存在便何。實際上,不存在真的不存在嗎?避無可避,終於要面對。
避到就是好,避唔到就是禍?未必如此。
終於發現了複數。但往後的發展十分緩慢,一直要過多兩三百年,Gauss、Argand 等人給出「複平面」,發展開始快得多,再由黎曼推上一個頂峰。
Saturday, October 17, 2009
從畢氏定理說起
最近看書,引發我從另一個角度看畢氏定理。

大家還記得畢氏定理吧?參看圖中的直角三角形,畢氏定理指出了三邊的關係:「a^2 + b^2 = c^2」。
中學時大家做過不少習題,知道符合這關係的 (a, b, c) 的值,有可能是漂亮的整數,如 (3, 4, 5),亦有可能不太漂亮,如 (2, 3, sqrt(13))。數學家對整數特別有興趣,把這些非零整數的 (a, b, c) 稱為 Pythagorean triples,如 (3, 4, 5), (5, 12, 13) 便是其中兩組。
現在我們把數式「a^2 + b^2 = c^2」變換一下。
把整個式子除以 c^2,得出
(a/c)^2 + (b/c)^2 = 1
設 x = (a/c), y = (b/c),得出
x^2 + y^2 = 1
似曾相識嗎?無錯,這是圓方程。下圖的紅色線,顯示該方程在第一象限中的圖像。
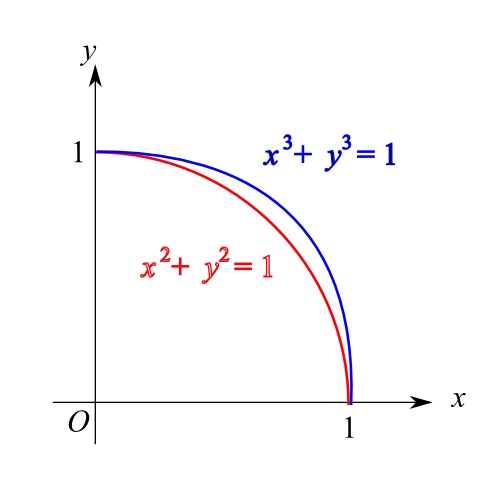
每個符合畢氏定理的 (a, b, c),均可化為該線上的一點。
而當中的 Pythagorean triples,便是該線上 x 坐標和 y 坐標均是非零有理數的點。
在數線上,不難想像任何兩個有理數之間,我們必定會找到無理數;任何兩個無理數之間,也可找到有理數。無理數與有理數,大家互相穿插其中。
平面上也應該差不多吧?
任意兩個有理的 x 坐標之間,必會出理無理的 x 坐標;任意兩個無理的 x 坐標之間,也必會出現有理的 x 坐標。
任意兩個有理的 y 坐標之間,必會出理無理的 y 坐標;任意兩個無理的 y 坐標之間,也必會出現有理的 y 坐標。
在 xy 平面上畫一條線,該線會通過一些 x, y 坐標均是有理數的點,不足為奇吧?
就像 x^2 + y^2 = 1 的圖像般。
真的嗎?
大家留意到圖中還有一條藍線吧?那是方程 x^3 + y^3 = 1 的圖像。
這條線也會通過一些 x, y 坐標均是非零有理數的點嗎?
答案是不會的。
點解?
費馬大定理
費馬大家理,幾百年前費馬的一個猜想,它猜測方程「a^n + b^n = c^n」當 n 是大於2的整數時,(a, b, c)不可能全是非零整數。這個猜想,一直到十多年前才得以證明。
把「a^n + b^n = c^n」全式除以 c^n,再如之前般設 x=a/c, y=b/c,得出
x^n + y^n =1。
若x, y 可以是有理數,把全式乘以 (x 和y 的 分母的 LCM)^n,便得可得出一組整數的 (a, b, c) 符合「a^n + b^n = c^n」,這與費馬大定理產生矛盾,所以是不可能的。
因此,
曲線 x^3 + y^3 =1 不會通過 x, y 坐標均是有理數的點。
曲線 x^4 + y^4 =1 不會通過 x, y 坐標均是有理數的點。
曲線 x^5 + y^5 =1 不會通過 x, y 坐標均是有理數的點。
.
.
.
只要 n 是大於 2 的整數,曲線 x^n + y^n =1 不會通過 x, y 坐標均是有理數的點。
神奇嗎?這兒有無數條曲線,都不會通過 x, y 坐標均是有理數的點!
雖然有理數、無理數均有無數個,但這樣看來,有理數與無理數相比,真是少得可憐。
數,是數論、代數問題。坐標,是幾何問題。很少會把兩者一併來看,是我的想像力太低吧。
如果 n 不是整數,例如 2.5, 3.334, 甚至是 sqrt(3)、Pi 等無理數,情況又會如何呢?我不知道。

大家還記得畢氏定理吧?參看圖中的直角三角形,畢氏定理指出了三邊的關係:「a^2 + b^2 = c^2」。
中學時大家做過不少習題,知道符合這關係的 (a, b, c) 的值,有可能是漂亮的整數,如 (3, 4, 5),亦有可能不太漂亮,如 (2, 3, sqrt(13))。數學家對整數特別有興趣,把這些非零整數的 (a, b, c) 稱為 Pythagorean triples,如 (3, 4, 5), (5, 12, 13) 便是其中兩組。
現在我們把數式「a^2 + b^2 = c^2」變換一下。
把整個式子除以 c^2,得出
(a/c)^2 + (b/c)^2 = 1
設 x = (a/c), y = (b/c),得出
x^2 + y^2 = 1
似曾相識嗎?無錯,這是圓方程。下圖的紅色線,顯示該方程在第一象限中的圖像。

每個符合畢氏定理的 (a, b, c),均可化為該線上的一點。
而當中的 Pythagorean triples,便是該線上 x 坐標和 y 坐標均是非零有理數的點。
在數線上,不難想像任何兩個有理數之間,我們必定會找到無理數;任何兩個無理數之間,也可找到有理數。無理數與有理數,大家互相穿插其中。
平面上也應該差不多吧?
任意兩個有理的 x 坐標之間,必會出理無理的 x 坐標;任意兩個無理的 x 坐標之間,也必會出現有理的 x 坐標。
任意兩個有理的 y 坐標之間,必會出理無理的 y 坐標;任意兩個無理的 y 坐標之間,也必會出現有理的 y 坐標。
在 xy 平面上畫一條線,該線會通過一些 x, y 坐標均是有理數的點,不足為奇吧?
就像 x^2 + y^2 = 1 的圖像般。
真的嗎?
大家留意到圖中還有一條藍線吧?那是方程 x^3 + y^3 = 1 的圖像。
這條線也會通過一些 x, y 坐標均是非零有理數的點嗎?
答案是不會的。
點解?
費馬大定理
費馬大家理,幾百年前費馬的一個猜想,它猜測方程「a^n + b^n = c^n」當 n 是大於2的整數時,(a, b, c)不可能全是非零整數。這個猜想,一直到十多年前才得以證明。
把「a^n + b^n = c^n」全式除以 c^n,再如之前般設 x=a/c, y=b/c,得出
x^n + y^n =1。
若x, y 可以是有理數,把全式乘以 (x 和y 的 分母的 LCM)^n,便得可得出一組整數的 (a, b, c) 符合「a^n + b^n = c^n」,這與費馬大定理產生矛盾,所以是不可能的。
因此,
曲線 x^3 + y^3 =1 不會通過 x, y 坐標均是有理數的點。
曲線 x^4 + y^4 =1 不會通過 x, y 坐標均是有理數的點。
曲線 x^5 + y^5 =1 不會通過 x, y 坐標均是有理數的點。
.
.
.
只要 n 是大於 2 的整數,曲線 x^n + y^n =1 不會通過 x, y 坐標均是有理數的點。
神奇嗎?這兒有無數條曲線,都不會通過 x, y 坐標均是有理數的點!
雖然有理數、無理數均有無數個,但這樣看來,有理數與無理數相比,真是少得可憐。
數,是數論、代數問題。坐標,是幾何問題。很少會把兩者一併來看,是我的想像力太低吧。
如果 n 不是整數,例如 2.5, 3.334, 甚至是 sqrt(3)、Pi 等無理數,情況又會如何呢?我不知道。
Sunday, August 09, 2009
R^2 and C
Sunday, July 12, 2009
Age, Quantity or Magnitude?
最近看書,該書的作者用數學的角度去解釋中國傳統用作計算年齡的「虛歲」與我們現今常用來計算年齡的「周歲、實歲」,我覺得都幾有道理。
周歲,很多人也很清楚吧?
一個人出生的那一刻,視為0歲。以周歲計算,那人在某刻的年齡就是與0歲相差的時間間距。
例如小明在2009年1月1日出生,到了2009年7月1日,小明便是半歲。而在2011年1月1日,小明便是兩歲。
而虛歲則較為混亂。可能會有各處鄉村各處例也不為奇。小時候我父母說把實歲加二便是虛歲,說是甚麼天給一歲地給一歲,聽得我一頭霧水。
有些人說虛歲要加一歲,有些人說虛歲要加兩歲。究竟虛歲是怎樣計算的?
後來我發現(從wiki),其實有一種更為人採用來計算虛歲的方法。那就是我們出生時視為一歲。然後每過一個春節便增加一歲。
例如小玲在農曆十二月三十日出生,出生時便已當一歲。一天後,即是正月初一,便視為兩歲了。
據該書的作者,西方傳統,或現時普遍來說,是把年齡視為一個量度的量(Magnitude),而中國傳統則視年齡為一個可數的量(Quantity)。
以圖像來表示,圖A代表實歲,圖B代表虛歲。
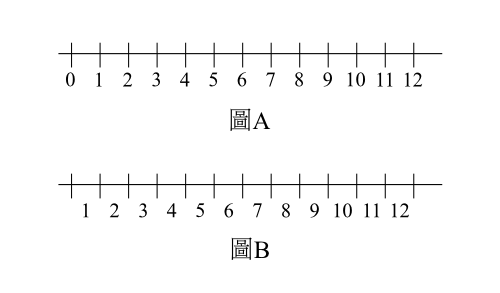
按實歲的說法,一個人現在是n歲,是指那人在世上活了n年。
而按虛歲的說法,一個人現在是n歲,是指今年是那人活在世上的第n個年頭。
兩個說法的字眼相似,但背後的概念其實不同。
我一直用實歲的概念去理解虛歲,所以覺得虛歲難以理解,覺得只是一些迷信、很「玄」的東西。但當知道背後的概念後,所有疑惑都一掃而空。
把自己的思維套進可數的量來理解虛歲,就會覺得虛歲系統也是很自然的事情。
點算東西,自古以來也是由一開始。出生的那一年,是你來到世上的第一個年頭,於是記為「一歲」。春節來到,代表踏入新的一年,亦即是你來到世上的第二個年頭,於是記為「兩歲」,如此類推。虛歲就是用來點算這個年頭是你活在世上的第幾年。你看按「可數的量」這概念,虛歲是否也很自然呢?
西方人把年歲看成一個量度的量,那麼是否所有與時間有關的量也視為量度的量呢?其實並不是。我們現在所用的公元記年系統,其實是把時間看成可數的量。
在公元系統,是沒有一個參考點與之相對來量度,即是沒有公元0之說,而是把耶穌出生的那個年頭記為公元一年。在過一年,即耶穌出生後的第二個年頭記為公元二年。一直這樣數下去。
而耶穌出生前的一個年頭記為公元前一年,再對上的一個年頭是公元前二年,如此類推。
(別對我說甚麼耶穌其實不是在那年那年出生。我的重點是總之把某年定為第一年,然後第二年第三年這樣數下去。)
****************************************************************
不知大家怎樣看可數的量(quantity)和量度的量(magnitude)?
在我讀書的年代,包括小學中學和大學,我也沒有意識去區分兩者的差異。
只是覺得一直以來所認識的數在擴充。所認識的數線,由最初零散的整數開始,後來包括有理數、無理數。甚至認識到數線以外的複數。
一直以來也習以為常使用這些「數」。
是甚麼時候開始有這個意識去區分 quantity 和 magnitude呢?
是早幾年前,開始想去理解「第一次數學危機」開始。
還記得甚麼是第一次數學危機嗎?中學時老師也有提過。
古希臘的數學家認為(柏拉圖時代),萬物階為數。
這個數是指正整數。我想是透過基本的四則混算,整數的加減乘也會得出整數。而除呢?得出分數。所以那時也承認整數之比,即有理數的存在。
但後來畢達哥拉斯學派(Pythagorean School)的其中一個信徒希柏斯(Hippasus)證明了一些數並不是整數,或整數之比。
這發現震撼了整個古希臘,史稱第一次數學危機。
中學時的我會問點解d古希臘人咁傻仔。
當時的我覺得(純是直覺的覺得,沒有甚麼理性根據),存在有盡小數,就存在無盡小數。有循環的,就會有不循環的。無理數可以表示為無盡不循環小數,所以無理數的存在是理所當然。
就算以前不知道有這類數,現在知道了,便接受吧。危機在哪裏?純粹因為希柏斯在古希臘的偉大哲學家臉上噴灰?那太沒有風度。
後來才知箇中原因。深入去看,我想是和古希臘的「原子論」(atomism)有關。
單從數學來看,是一直以來古希臘人所發展出「比」(ratio)的概念,也依賴著「所有數皆是整數或整數之比」,而很多幾何命題的證明也依靠這些比的知識。如果「所有數皆是整數或整數之比」不成立,意味著很多幾何知識的根基也不可靠。
如何解決?
Eudoxus 修正了「比」的概念,把古希臘的幾何拯救出來。歐幾里得的幾何原本也中關於比的一章,據說很多材料也來自Eudoxus的知識。
以往古希臘的代數與幾可密一可分。但經此一役,醒覺到數(可數的量)與幾何量(量度的量)的差異,代數與幾何從此分家。
(本來這個題目我還有很多野想講,但想下想下,實在會有太多野寫下去,我想都沒有太多人有興趣去看,自己近來寫blog也很慢,沒甚麼心力去寫一篇長文。希望總有一天我會寫出來吧。)
(註:文中開首時我所提及我看的那本書是《質數魔力》(Prime Obsession)。)
周歲,很多人也很清楚吧?
一個人出生的那一刻,視為0歲。以周歲計算,那人在某刻的年齡就是與0歲相差的時間間距。
例如小明在2009年1月1日出生,到了2009年7月1日,小明便是半歲。而在2011年1月1日,小明便是兩歲。
而虛歲則較為混亂。可能會有各處鄉村各處例也不為奇。小時候我父母說把實歲加二便是虛歲,說是甚麼天給一歲地給一歲,聽得我一頭霧水。
有些人說虛歲要加一歲,有些人說虛歲要加兩歲。究竟虛歲是怎樣計算的?
後來我發現(從wiki),其實有一種更為人採用來計算虛歲的方法。那就是我們出生時視為一歲。然後每過一個春節便增加一歲。
例如小玲在農曆十二月三十日出生,出生時便已當一歲。一天後,即是正月初一,便視為兩歲了。
據該書的作者,西方傳統,或現時普遍來說,是把年齡視為一個量度的量(Magnitude),而中國傳統則視年齡為一個可數的量(Quantity)。
以圖像來表示,圖A代表實歲,圖B代表虛歲。

按實歲的說法,一個人現在是n歲,是指那人在世上活了n年。
而按虛歲的說法,一個人現在是n歲,是指今年是那人活在世上的第n個年頭。
兩個說法的字眼相似,但背後的概念其實不同。
我一直用實歲的概念去理解虛歲,所以覺得虛歲難以理解,覺得只是一些迷信、很「玄」的東西。但當知道背後的概念後,所有疑惑都一掃而空。
把自己的思維套進可數的量來理解虛歲,就會覺得虛歲系統也是很自然的事情。
點算東西,自古以來也是由一開始。出生的那一年,是你來到世上的第一個年頭,於是記為「一歲」。春節來到,代表踏入新的一年,亦即是你來到世上的第二個年頭,於是記為「兩歲」,如此類推。虛歲就是用來點算這個年頭是你活在世上的第幾年。你看按「可數的量」這概念,虛歲是否也很自然呢?
西方人把年歲看成一個量度的量,那麼是否所有與時間有關的量也視為量度的量呢?其實並不是。我們現在所用的公元記年系統,其實是把時間看成可數的量。
在公元系統,是沒有一個參考點與之相對來量度,即是沒有公元0之說,而是把耶穌出生的那個年頭記為公元一年。在過一年,即耶穌出生後的第二個年頭記為公元二年。一直這樣數下去。
而耶穌出生前的一個年頭記為公元前一年,再對上的一個年頭是公元前二年,如此類推。
(別對我說甚麼耶穌其實不是在那年那年出生。我的重點是總之把某年定為第一年,然後第二年第三年這樣數下去。)
****************************************************************
不知大家怎樣看可數的量(quantity)和量度的量(magnitude)?
在我讀書的年代,包括小學中學和大學,我也沒有意識去區分兩者的差異。
只是覺得一直以來所認識的數在擴充。所認識的數線,由最初零散的整數開始,後來包括有理數、無理數。甚至認識到數線以外的複數。
一直以來也習以為常使用這些「數」。
是甚麼時候開始有這個意識去區分 quantity 和 magnitude呢?
是早幾年前,開始想去理解「第一次數學危機」開始。
還記得甚麼是第一次數學危機嗎?中學時老師也有提過。
古希臘的數學家認為(柏拉圖時代),萬物階為數。
這個數是指正整數。我想是透過基本的四則混算,整數的加減乘也會得出整數。而除呢?得出分數。所以那時也承認整數之比,即有理數的存在。
但後來畢達哥拉斯學派(Pythagorean School)的其中一個信徒希柏斯(Hippasus)證明了一些數並不是整數,或整數之比。
這發現震撼了整個古希臘,史稱第一次數學危機。
中學時的我會問點解d古希臘人咁傻仔。
當時的我覺得(純是直覺的覺得,沒有甚麼理性根據),存在有盡小數,就存在無盡小數。有循環的,就會有不循環的。無理數可以表示為無盡不循環小數,所以無理數的存在是理所當然。
就算以前不知道有這類數,現在知道了,便接受吧。危機在哪裏?純粹因為希柏斯在古希臘的偉大哲學家臉上噴灰?那太沒有風度。
後來才知箇中原因。深入去看,我想是和古希臘的「原子論」(atomism)有關。
單從數學來看,是一直以來古希臘人所發展出「比」(ratio)的概念,也依賴著「所有數皆是整數或整數之比」,而很多幾何命題的證明也依靠這些比的知識。如果「所有數皆是整數或整數之比」不成立,意味著很多幾何知識的根基也不可靠。
如何解決?
Eudoxus 修正了「比」的概念,把古希臘的幾何拯救出來。歐幾里得的幾何原本也中關於比的一章,據說很多材料也來自Eudoxus的知識。
以往古希臘的代數與幾可密一可分。但經此一役,醒覺到數(可數的量)與幾何量(量度的量)的差異,代數與幾何從此分家。
(本來這個題目我還有很多野想講,但想下想下,實在會有太多野寫下去,我想都沒有太多人有興趣去看,自己近來寫blog也很慢,沒甚麼心力去寫一篇長文。希望總有一天我會寫出來吧。)
(註:文中開首時我所提及我看的那本書是《質數魔力》(Prime Obsession)。)
Sunday, June 28, 2009
Square root of 2 to the power of square root of 2
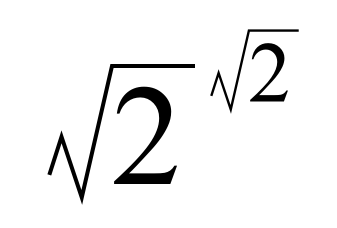
最近讀到一個令我幾迷惘的數學證明。迷惘的並不是它涉及甚麼高深的數學知識,其實只須具備初中有關指數和無理數的知識便可看懂。迷惘在於我看完個證明,好像甚麼也沒有得到似的。
看這證明之前,看看以下問題。
設 a 和 b 為無理數。下列各數式是否必定為無理數?
1. a+b
2. a-b
3. a*b
4. a/b
四條的答案都是否。相信大家也很容易舉出例子吧。
例如設 a=b=sqrt(2),那麼2,3,4的結果很明顯是有理數。
但這個數式又如何呢?
a^b (a 的 b 次方根, a to the power of b)
我想不出答案來。書本上提供了一個很簡潔的證明:
(首先,大家都不會質疑 sqrt(2) 是無理數吧?不相信?網上你會找到很多資料,我不多講了。)
如果 (sqrt(2))^sqrt(2) 是有理數,那麼我們便即找到無理數a和b(即a=b=sqrt(2))使a^b是有理數。
如果 (sqrt(2))^sqrt(2) 是無理數,設 a=(sqrt(2))^sqrt(2), b=sqrt(2)
a^b
=((sqrt(2))^sqrt(2))^sqrt(2)
=(sqrt(2))^(sqrt(2) * sqrt(2))
=(sqrt(2))^2
=2
即a^b是有理數
證明頗簡潔吧?我們證明了存在無理數a和b使a^b為有理數。
但我總覺得欠缺了些東西,就是看罷證明後,我也不能舉出一個實在的例子來印證。
多年來我是否首次遇上這種證明的技巧?我不清楚。
可能讀大學時也會遇過,不過或許涉及的東西我不太感興趣,所以也沒有去深究。
但這個對象是有理數和無理數,中學時代也有接觸,我們也常常用到,因此引起我的注意。
一直以來我都覺得「證明到要證明的東西」不是證明的最主要功用,不過這個例子實在太極端了。除了證明到要證明的東西,這個例子可說是毫無建設性。
如果有人用以上形式建構出以下證明,你有甚麼想法?
如果神存在,那麼abc...
如果神不存在,那麼xyz...
因此,神是存在的。
神,在哪裏?
Sunday, June 21, 2009
解
上一個題目,我還未想得出一個不用計算的答案。
以下是我的計算答案:
先考慮黑色部分,它可分成內、外兩部分。
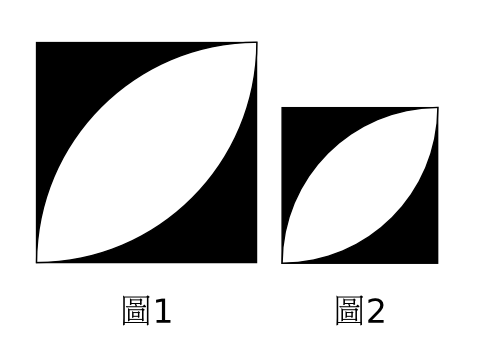
看看外部,把它分拆重組,可得出兩個圖1般的圖形。
而內部,很明顯是由四個圖2般的圖形組成。
再考慮原圖,用畢氏定理,我們可發現圖1和圖2的正方形邊長之比是 1:sqrt(2)
(看不出來?設原圖紅色圓形的半徑為 sqrt(2)。sqrt(2) 即是 positive sqare root of 2, 2的正平方根。)
知道這個比是很重要的。由於圖1和圖2是相似圖形,所以面積之比即是邊長之比的平方。因此圖1的面積是圖2的面積的2倍。
外部有2個圖1,內部有4個圖2,因此內、外的黑色部分面積相同。
仍是考慮原圖。設大正方形的邊長為2。很明顯,正方形面積減圓面積便可得外部黑色部分的面積。
因此外部黑色部分的面積是 4-pi
而內部黑色部分的面積也是4-pi
所以黑色部分總面積是8-2pi
紅色部分的面積呢?
把圓面積減去內部黑色部分的面積便可求得。
即是 pi-(4-pi) = 2pi-4
因此,黑色部分的面積:紅色部分的面積是
(8-2pi) : (2pi -4)
紅色部分面積較大
以下是我的計算答案:
先考慮黑色部分,它可分成內、外兩部分。

看看外部,把它分拆重組,可得出兩個圖1般的圖形。
而內部,很明顯是由四個圖2般的圖形組成。
再考慮原圖,用畢氏定理,我們可發現圖1和圖2的正方形邊長之比是 1:sqrt(2)
(看不出來?設原圖紅色圓形的半徑為 sqrt(2)。sqrt(2) 即是 positive sqare root of 2, 2的正平方根。)
知道這個比是很重要的。由於圖1和圖2是相似圖形,所以面積之比即是邊長之比的平方。因此圖1的面積是圖2的面積的2倍。
外部有2個圖1,內部有4個圖2,因此內、外的黑色部分面積相同。
仍是考慮原圖。設大正方形的邊長為2。很明顯,正方形面積減圓面積便可得外部黑色部分的面積。
因此外部黑色部分的面積是 4-pi
而內部黑色部分的面積也是4-pi
所以黑色部分總面積是8-2pi
紅色部分的面積呢?
把圓面積減去內部黑色部分的面積便可求得。
即是 pi-(4-pi) = 2pi-4
因此,黑色部分的面積:紅色部分的面積是
(8-2pi) : (2pi -4)
紅色部分面積較大
Subscribe to:
Posts (Atom)