Square root of 2 to the power of square root of 2

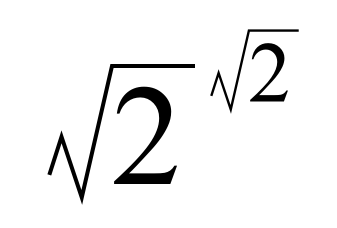
最近讀到一個令我幾迷惘的數學證明。迷惘的並不是它涉及甚麼高深的數學知識，其實只須具備初中有關指數和無理數的知識便可看懂。迷惘在於我看完個證明，好像甚麼也沒有得到似的。

看這證明之前，看看以下問題。

設 a 和 b 為無理數。下列各數式是否必定為無理數？
1. a+b
2. a-b
3. a*b
4. a/b

四條的答案都是否。相信大家也很容易舉出例子吧。
例如設 a=b=sqrt(2)，那麼2,3,4的結果很明顯是有理數。
但這個數式又如何呢？
a^b (a 的 b 次方根, a to the power of b)
我想不出答案來。書本上提供了一個很簡潔的證明：
(首先，大家都不會質疑 sqrt(2) 是無理數吧？不相信？網上你會找到很多資料，我不多講了。)
如果 (sqrt(2))^sqrt(2) 是有理數，那麼我們便即找到無理數a和b(即a=b=sqrt(2))使a^b是有理數。
如果 (sqrt(2))^sqrt(2) 是無理數，設 a=(sqrt(2))^sqrt(2), b=sqrt(2)
a^b
=((sqrt(2))^sqrt(2))^sqrt(2)
=(sqrt(2))^(sqrt(2) * sqrt(2))
=(sqrt(2))^2
=2
即a^b是有理數

證明頗簡潔吧？我們證明了存在無理數a和b使a^b為有理數。
但我總覺得欠缺了些東西，就是看罷證明後，我也不能舉出一個實在的例子來印證。
多年來我是否首次遇上這種證明的技巧？我不清楚。
可能讀大學時也會遇過，不過或許涉及的東西我不太感興趣，所以也沒有去深究。
但這個對象是有理數和無理數，中學時代也有接觸，我們也常常用到，因此引起我的注意。

一直以來我都覺得「證明到要證明的東西」不是證明的最主要功用，不過這個例子實在太極端了。除了證明到要證明的東西，這個例子可說是毫無建設性。

如果有人用以上形式建構出以下證明，你有甚麼想法？
如果神存在，那麼abc...
如果神不存在，那麼xyz...
因此，神是存在的。




神，在哪裏？