解

上一個題目，我還未想得出一個不用計算的答案。
以下是我的計算答案：

先考慮黑色部分，它可分成內、外兩部分。



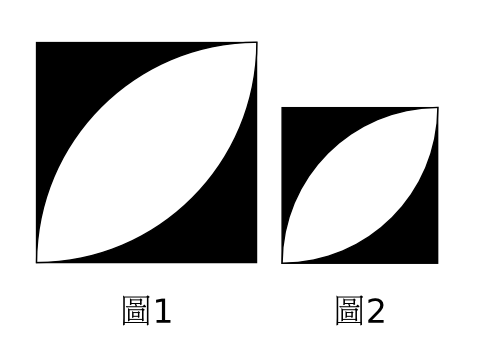
看看外部，把它分拆重組，可得出兩個圖1般的圖形。
而內部，很明顯是由四個圖2般的圖形組成。

再考慮原圖，用畢氏定理，我們可發現圖1和圖2的正方形邊長之比是 1:sqrt(2)
(看不出來？設原圖紅色圓形的半徑為 sqrt(2)。sqrt(2) 即是 positive sqare root of 2, 2的正平方根。)
知道這個比是很重要的。由於圖1和圖2是相似圖形，所以面積之比即是邊長之比的平方。因此圖1的面積是圖2的面積的2倍。
外部有2個圖1，內部有4個圖2，因此內、外的黑色部分面積相同。

仍是考慮原圖。設大正方形的邊長為2。很明顯，正方形面積減圓面積便可得外部黑色部分的面積。
因此外部黑色部分的面積是 4-pi
而內部黑色部分的面積也是4-pi
所以黑色部分總面積是8-2pi

紅色部分的面積呢？
把圓面積減去內部黑色部分的面積便可求得。
即是 pi-(4-pi) = 2pi-4
因此，黑色部分的面積:紅色部分的面積是
(8-2pi) : (2pi -4)
紅色部分面積較大