周歲,很多人也很清楚吧?
一個人出生的那一刻,視為0歲。以周歲計算,那人在某刻的年齡就是與0歲相差的時間間距。
例如小明在2009年1月1日出生,到了2009年7月1日,小明便是半歲。而在2011年1月1日,小明便是兩歲。
而虛歲則較為混亂。可能會有各處鄉村各處例也不為奇。小時候我父母說把實歲加二便是虛歲,說是甚麼天給一歲地給一歲,聽得我一頭霧水。
有些人說虛歲要加一歲,有些人說虛歲要加兩歲。究竟虛歲是怎樣計算的?
後來我發現(從wiki),其實有一種更為人採用來計算虛歲的方法。那就是我們出生時視為一歲。然後每過一個春節便增加一歲。
例如小玲在農曆十二月三十日出生,出生時便已當一歲。一天後,即是正月初一,便視為兩歲了。
據該書的作者,西方傳統,或現時普遍來說,是把年齡視為一個量度的量(Magnitude),而中國傳統則視年齡為一個可數的量(Quantity)。
以圖像來表示,圖A代表實歲,圖B代表虛歲。
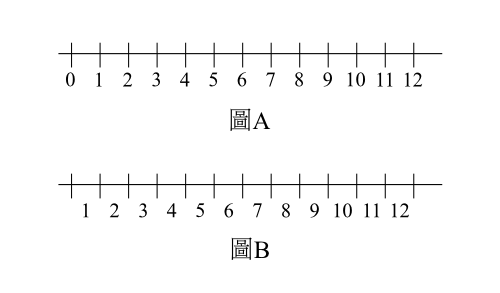
按實歲的說法,一個人現在是n歲,是指那人在世上活了n年。
而按虛歲的說法,一個人現在是n歲,是指今年是那人活在世上的第n個年頭。
兩個說法的字眼相似,但背後的概念其實不同。
我一直用實歲的概念去理解虛歲,所以覺得虛歲難以理解,覺得只是一些迷信、很「玄」的東西。但當知道背後的概念後,所有疑惑都一掃而空。
把自己的思維套進可數的量來理解虛歲,就會覺得虛歲系統也是很自然的事情。
點算東西,自古以來也是由一開始。出生的那一年,是你來到世上的第一個年頭,於是記為「一歲」。春節來到,代表踏入新的一年,亦即是你來到世上的第二個年頭,於是記為「兩歲」,如此類推。虛歲就是用來點算這個年頭是你活在世上的第幾年。你看按「可數的量」這概念,虛歲是否也很自然呢?
西方人把年歲看成一個量度的量,那麼是否所有與時間有關的量也視為量度的量呢?其實並不是。我們現在所用的公元記年系統,其實是把時間看成可數的量。
在公元系統,是沒有一個參考點與之相對來量度,即是沒有公元0之說,而是把耶穌出生的那個年頭記為公元一年。在過一年,即耶穌出生後的第二個年頭記為公元二年。一直這樣數下去。
而耶穌出生前的一個年頭記為公元前一年,再對上的一個年頭是公元前二年,如此類推。
(別對我說甚麼耶穌其實不是在那年那年出生。我的重點是總之把某年定為第一年,然後第二年第三年這樣數下去。)
****************************************************************
不知大家怎樣看可數的量(quantity)和量度的量(magnitude)?
在我讀書的年代,包括小學中學和大學,我也沒有意識去區分兩者的差異。
只是覺得一直以來所認識的數在擴充。所認識的數線,由最初零散的整數開始,後來包括有理數、無理數。甚至認識到數線以外的複數。
一直以來也習以為常使用這些「數」。
是甚麼時候開始有這個意識去區分 quantity 和 magnitude呢?
是早幾年前,開始想去理解「第一次數學危機」開始。
還記得甚麼是第一次數學危機嗎?中學時老師也有提過。
古希臘的數學家認為(柏拉圖時代),萬物階為數。
這個數是指正整數。我想是透過基本的四則混算,整數的加減乘也會得出整數。而除呢?得出分數。所以那時也承認整數之比,即有理數的存在。
但後來畢達哥拉斯學派(Pythagorean School)的其中一個信徒希柏斯(Hippasus)證明了一些數並不是整數,或整數之比。
這發現震撼了整個古希臘,史稱第一次數學危機。
中學時的我會問點解d古希臘人咁傻仔。
當時的我覺得(純是直覺的覺得,沒有甚麼理性根據),存在有盡小數,就存在無盡小數。有循環的,就會有不循環的。無理數可以表示為無盡不循環小數,所以無理數的存在是理所當然。
就算以前不知道有這類數,現在知道了,便接受吧。危機在哪裏?純粹因為希柏斯在古希臘的偉大哲學家臉上噴灰?那太沒有風度。
後來才知箇中原因。深入去看,我想是和古希臘的「原子論」(atomism)有關。
單從數學來看,是一直以來古希臘人所發展出「比」(ratio)的概念,也依賴著「所有數皆是整數或整數之比」,而很多幾何命題的證明也依靠這些比的知識。如果「所有數皆是整數或整數之比」不成立,意味著很多幾何知識的根基也不可靠。
如何解決?
Eudoxus 修正了「比」的概念,把古希臘的幾何拯救出來。歐幾里得的幾何原本也中關於比的一章,據說很多材料也來自Eudoxus的知識。
以往古希臘的代數與幾可密一可分。但經此一役,醒覺到數(可數的量)與幾何量(量度的量)的差異,代數與幾何從此分家。
(本來這個題目我還有很多野想講,但想下想下,實在會有太多野寫下去,我想都沒有太多人有興趣去看,自己近來寫blog也很慢,沒甚麼心力去寫一篇長文。希望總有一天我會寫出來吧。)
(註:文中開首時我所提及我看的那本書是《質數魔力》(Prime Obsession)。)
No comments:
Post a Comment