從畢氏定理說起

最近看書，引發我從另一個角度看畢氏定理。


大家還記得畢氏定理吧？參看圖中的直角三角形，畢氏定理指出了三邊的關係：「a^2 + b^2 = c^2」。
中學時大家做過不少習題，知道符合這關係的 (a, b, c) 的值，有可能是漂亮的整數，如 (3, 4, 5)，亦有可能不太漂亮，如 (2, 3, sqrt(13))。數學家對整數特別有興趣，把這些非零整數的 (a, b, c) 稱為 Pythagorean triples，如 (3, 4, 5), (5, 12, 13) 便是其中兩組。

現在我們把數式「a^2 + b^2 = c^2」變換一下。
把整個式子除以 c^2，得出
(a/c)^2 + (b/c)^2 = 1
設 x = (a/c), y = (b/c)，得出
x^2 + y^2 = 1
似曾相識嗎？無錯，這是圓方程。下圖的紅色線，顯示該方程在第一象限中的圖像。

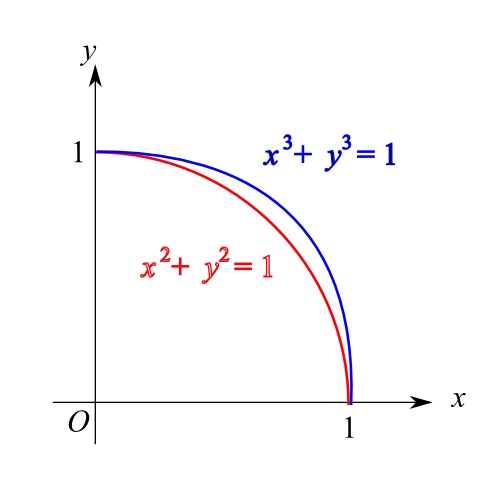
每個符合畢氏定理的 (a, b, c)，均可化為該線上的一點。
而當中的 Pythagorean triples，便是該線上 x 坐標和 y 坐標均是非零有理數的點。
在數線上，不難想像任何兩個有理數之間，我們必定會找到無理數；任何兩個無理數之間，也可找到有理數。無理數與有理數，大家互相穿插其中。
平面上也應該差不多吧？
任意兩個有理的 x 坐標之間，必會出理無理的 x 坐標；任意兩個無理的 x 坐標之間，也必會出現有理的 x 坐標。
任意兩個有理的 y 坐標之間，必會出理無理的 y 坐標；任意兩個無理的 y 坐標之間，也必會出現有理的 y 坐標。
在 xy 平面上畫一條線，該線會通過一些 x, y 坐標均是有理數的點，不足為奇吧？
就像 x^2 + y^2 = 1 的圖像般。

真的嗎？
大家留意到圖中還有一條藍線吧？那是方程 x^3 + y^3 = 1 的圖像。
這條線也會通過一些 x, y 坐標均是非零有理數的點嗎？
答案是不會的。
點解？
費馬大定理
費馬大家理，幾百年前費馬的一個猜想，它猜測方程「a^n + b^n = c^n」當 n 是大於2的整數時，(a, b, c)不可能全是非零整數。這個猜想，一直到十多年前才得以證明。
把「a^n + b^n = c^n」全式除以 c^n，再如之前般設 x=a/c, y=b/c，得出
x^n + y^n =1。
若x, y 可以是有理數，把全式乘以 (x 和y 的 分母的 LCM)^n，便得可得出一組整數的 (a, b, c) 符合「a^n + b^n = c^n」，這與費馬大定理產生矛盾，所以是不可能的。
因此，
曲線 x^3 + y^3 =1 不會通過 x, y 坐標均是有理數的點。
曲線 x^4 + y^4 =1 不會通過 x, y 坐標均是有理數的點。
曲線 x^5 + y^5 =1 不會通過 x, y 坐標均是有理數的點。
.
.
.
只要 n 是大於 2 的整數，曲線 x^n + y^n =1 不會通過 x, y 坐標均是有理數的點。

神奇嗎？這兒有無數條曲線，都不會通過 x, y 坐標均是有理數的點！
雖然有理數、無理數均有無數個，但這樣看來，有理數與無理數相比，真是少得可憐。

數，是數論、代數問題。坐標，是幾何問題。很少會把兩者一併來看，是我的想像力太低吧。

如果 n 不是整數，例如 2.5, 3.334, 甚至是 sqrt(3)、Pi 等無理數，情況又會如何呢？我不知道。