柏拉圖立體2

上一篇有關柏拉圖立體的文章，提到古希臘人發現只存在五種柏拉圖立體。沒有多，沒有少，恰好是五種。你有沒有想過當中的原因呢？

看看我的思想實驗吧。

還記得我所提的柏拉圖立體的定義嗎？每個頂點都是由相同數目的面相交而成。就由這個資料出發。

下圖我嘗試把所有可能情況窮舉出來：

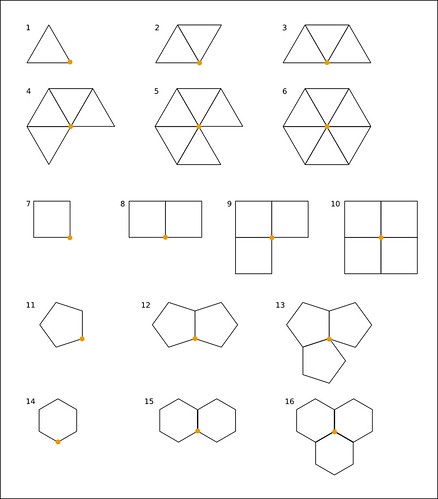
圖中圓點代表多面體的頂點。
由等邊三角形面開始，然後是正方形，跟著是正五邊形，再來是正六邊形。
很明顯，只有一或兩個面是不能相交成多面體的頂點。
因此，圖 1, 2, 7, 8, 11, 12, 14, 15 可以剔除。
圖 6, 10, 16，那幾個多邊形面剛好填滿平面，不能「屈成」一個立體的角，可以剔除。

可不可以有一個頂點由七個或以上的等邊三角形面組成嗎？剪張紙試試，你會發現不能屈起成一個立體角。
同理，四個或以上的正五邊形/正六邊形面，都是不可行。
三個或以上的正 n 邊形(n>7)也是不可行。

剩下哪幾個圖？就是 3, 4, 5, 9, 13
看！他們正是分別對應於正四面體、正八面體、正二十面體、正方體、正十二面體，這五種柏拉圖立體的結構。無錯，就是只有這五種，無多無少。

這個思想實驗，不是甚麼嚴謹證明，但我想大部分人直觀上也可以接受。例如「不能屈成一個立體的角」，直觀上也很易接受吧。

我第一次看這命題的證明，是要用到歐拉公式再加上窮舉法得出來。但其實要嚴謹證明歐拉公式，我也不懂。反正要窮舉，有沒有可能窮舉得易明一些？就想出這個思想實驗。