西九

無無聊聊，去西九逛逛。


ICC 快將完工吧。他朝一日，會與對岸的 IFC 成為香港兩枝頂心杉。


海風吹拂著岸邊小草，很舒服。





這種花有何特別之處？牡丹雖好，也要綠葉扶持。無錯，就是欠缺了綠葉。


到了這個季節，已很少看見這種黃花了。




看見嗎？那些小花組成一副得意的樣子。






西九海濱長廊，其實不太美，圍爛外你會看見很多爛地，不過很寧靜、很舒服。
不過今天去到，這片寧靜給打破了。四圍很多人在踏單車，很多小孩衝呀衝。其實我覺得在這兒踏單車很危險，單車徑很窄，我想兩個死肥仔打橫行已佔了單車徑。於是，很多人在旁邊的木板路上踏單車。但那些木板不平，衝得快遇上凹凸處會很易炒車。加上今天有部分範圍正在佈置將會舉行的香港美酒佳肴巡禮，空間少了，踏單車更危險。

Astro Boy

這種裝置我覺得很有趣。不過四圍太光吧，效果不明顯。

看完這實驗室，順便去看電影阿童木。
之前我沒有看過阿童木的漫畫和動畫。起初我還以為這是日本製作，原來是荷里活的製品。
故事是關於阿童木的誕生。一部很正能量的電影。我覺得大人去看會有令大人感動的地方，小孩子去看會有小孩子喜歡的地方，看片時不斷傳來小孩的歡笑聲 :) 完場時還有人拍手！要知道，這間是荃灣百老匯，不是百老匯電影中心！第一次在電影中心以外的戲院完場時聽見有人鼓掌。

如果你想看官能刺激，這部電影絕對滿足唔到你。講3D，沒有3D眼鏡，亦沒有誇啦啦的 CG 效果，更沒有震撼的音效。但你用心去感受，絕對是一部觸動心靈的電影。平實的畫面朔造出溫馨的氣氛，適當的配樂絕對能牽引著觀眾的情緒。

3D 、音效，純粹是錦上添花，一部有主題的電影，就算是黑白雪花片，也能感動觀眾。

主題是甚麼？是愛。對這個世界的愛。愛，可以打破階級的隔膜，打破人與人間的不信任，打破欲望的枷鎖……很空範？我不想透露劇情，大家入場用心感受吧。

唯一要彈的，就是現在在香港上映的動畫，很難找到原裝配音來看。以前通常港島的 IFC、金鐘 UA、時代 UA 都會上映原裝版。這部阿童木，好像只有東涌有上映英文版配音。中文配音很多時也是生硬沒有感情。就算原裝是日文我不會聽得懂，但也可以感受到角色的感情。中文配音……不加上港式爛 gag 已算執到。

複數的出現

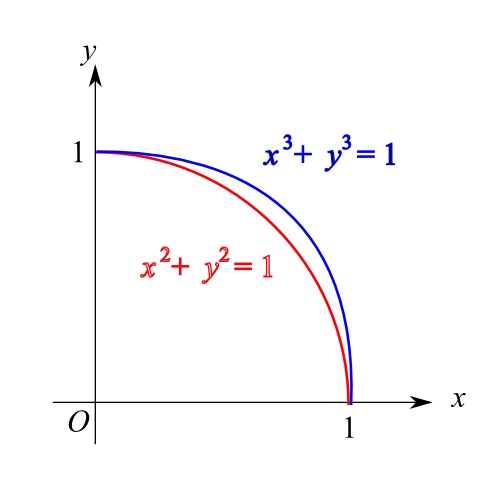
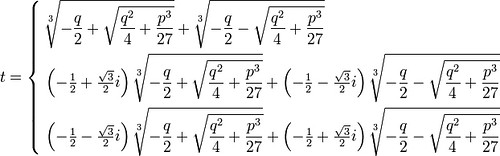大家還記得學習複數 (complex number) 時，書本上是怎樣引入的呢？
通常是：
數學家在研究三次方程 (cubic equation) 的求根公式時，發現了複數……
又或者
為了使 x^2 = -1, x^2 = -2......等方程有解，於是引入 i = sqrt(-1)
輕輕地交代了複數的發現，然後，大家便利用 i^2 = -1 這規則，再加上一直以來在實數四則運算見慣的交換律、分配律，進行複數的運算。

我想大約在我讀預科時，我「相信」複數是由數學家研究三次方程時開始被重視，因為我見過很多書都係咁講。而「為了使 x^2=-1, x^2=-2......等方程有解，於是引入 i=sqrt(-1)」只是一些書本簡便起見作出的引子吧。
那是我只是信，相信權威吧，但沒有其他理性上的理據說服到我。

當時我心入面有幾個問題：
1. 為甚麼要把 a+bi 看作「複數」，單單處理「bi」不行嗎？隨著接觸數學越來越多，我知道以「a+bi」作一個整體來看待，會引發出往後數學上很多豐盛的成果。
2. 為甚麼是在求「三次」方程才開以注意到複數？其實在二次方程的求根公式，有時都需要處理開方根號內帶有負數的問題 (即二次方程的判別式 b^2 - 4ac < 0)。

到近年 (近兩三年吧，近兩三年無乜時間觀念，忘了是何時了)，我才想出一個令我接受的原因。
(這個純粹是我令自己接受的原因，未必是正確的原因，我也沒有去考究現今主流研究數學史的學者是否抱著這觀點。)

先看二次方程的情況。我們可把二次方程 ax^2 + bx + c =0 寫成
x^2 - mx - n = 0, 其中 m = -(b/a), n = -(c/a)
移項得出
x^2 = mx + n
好戲在後頭，引入未知數 y，得出以下聯立方程：
y = x^2 及 y = mx + n
原來的二次方程的根，便是這個方程組中 x 的解了。點解我要咁做？我想在直角坐標平面上「看」二次方程的解。



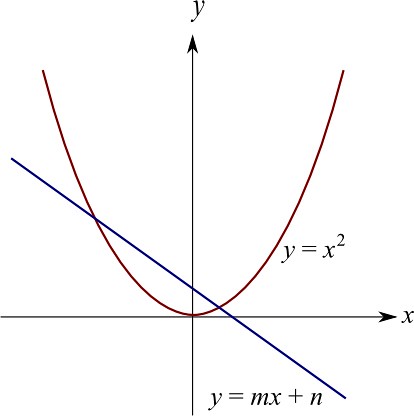
圖中顯示出 y = x^2 與 y = mx + n 的圖像。交點的 x 坐標便是原本二次方程的解。

不難想像，不同的 m 和 n 的值，就可代表不同的二次方程。
圖像中，y=x^2 這拋物線不變，改變直線 (即 m 和 n 的值)，就可代表了不同的二次方程。大家有否發現，不是所有直線都與拋物線有交點？例如把我的附圖中的直線往下移，便會得出一條與拋物線不相交的直線。

沒有交點，即是方程無解吧！也就是判別式 b^2 - 4ac < 0。
因此，在解二次方程時，若 b^2 - 4ac < 0，我們可以不去深究 sqrt(b^2 - 4ac) 究竟是甚麼。無解就是無解啦，無交點就是無交點啦，不存在就是不存在啦，何須自找麻煩去研究這些不存在的東西？

真的不用理嗎？看看三次方程的情況。
三次方程 x^3 + ax^2 + bx + c = 0，可以變換為
t^3 + pt + q = 0 (設 t = x - a/3 )
與二次方程的做法相似，改寫成
y = t^3 及 y = - pt - q
這樣便可在 yt 平面上觀察解的情況。

下圖是 y = t^3 的圖像：



這三次函數的圖像，與二次函數 y = x^2 的圖像有一個很明顯的分別，就是沒有最低點。
給定任意一個 y 值，我們都可以找到圖像上對應的 t 值。當在圖上加上直線，必定會與曲線相交！這代表著三次方程「必定」有解。

但看看三次方程 t^3 + pt + q = 0 的求根公式：



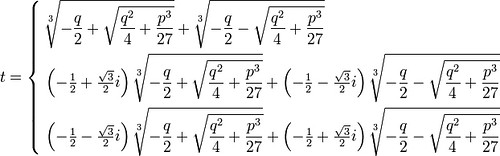
這公式我是在 wiki 抓下來，三個公式中，都有 sqrt((q^2)/4 + (p^3)/27) 這項。
設 q = 0, p=3，代入第一個公式，我們得出 t = 0 是一個解，是方程 t^3 + 3t = 0 的一個解。這個解與我們用因式分解得出的結果是一致的！

就係咁簡單？還未完。

看看方程 t^3 - 57t + 56 = 0，大家可把 t = -8, 1, 7 代入方程，發現它們是該方程的根。
繪畫 y = t^3 與 y = 57t - 56 的圖像，它們會於 t = -8, 1, 7 三處相交！

但是，把 p = -57 及 q = 56 代入求根公式，
會發現 (q^2)/4 + (p^3)/27 = -6075，即 sqrt((q^2)/4 + (p^3)/27) = sqrt(-6075) 不是實數
在第一個公式會得出
(-28 + sqrt(-6075))^(1/3) + (-28 - sqrt(-6075))^(1/3)
注意在第一個公式中，本身沒有複數。但我們看到要利用這公式求得這方程的解(實數)，我們先要懂得處理負數的開方根及有關的運算，即是複數的運算！(以上式子的結果為 7)

二次方程中，若 b^2 - 4ac < 0，公式涉及 sqrt(負數)，我們說方程無解，結果與圖像無交點是一致的。

而三次方程中，若 (q^2)/4 + (p^3)/27 < 0，公式涉及 sqrt(負數)，但我們不能就此指出方程無解，這會與圖像有交點的程況不一致！

這次，我們無得再逃避了，要達到求三次方程的根這個目標，必先要好好研究這類「新」的數的運算！

就是這個圖像上的原因，令我接受書本上所謂由解三次方程開始才重視複數的事實。

這原因是對？是錯？我不知。很大程度取決於當時數學家怎樣看方程的圖像這概念。事實上，坐標幾何的出現，現今歸功於十七世紀笛卡兒 (Rene Descartes, 1596 - 1650) 的貢獻，這是在三次方程求根公式之後發生的事情。不過數學發展不是石頭爆出來的，之前都有很多痕跡可尋。例如遠在古希臘的阿波羅尼奧斯 (Apollonius, 262BC - 196 BC)，他處理圓錐曲線的一些技巧與現今坐標幾何的方法相近。所以我覺得15、16 世紀數學家是從圖像令他們不重視二次方程的複數解，但在三次方程時要認真處理，也不足為奇。

世事就是咁神奇，以為可以避開，當佢不存在便何。實際上，不存在真的不存在嗎？避無可避，終於要面對。
避到就是好，避唔到就是禍？未必如此。

終於發現了複數。但往後的發展十分緩慢，一直要過多兩三百年，Gauss、Argand 等人給出「複平面」，發展開始快得多，再由黎曼推上一個頂峰。

十年

最近 youtube 一段片，全城熱爆，不知大家有沒有看過？
按我看片
對白如下：
「我唔係無試過，我試過安份守己，日搏夜搏，賺o個一萬幾千。我試過。但出面o個班人，出面o個班人呀，佢地識建築識起樓咩？佢地只係攞少少錢出o黎，攞少少時間，炒起個樓市就不停係到賺大錢，咁叫公平咩？

你出去問下人，是但問一個人，問下佢地需要d乜野，佢地答案好簡單，只係需要一間好普通好普通gei樓。點解佢地要用成世人gei時間去供一層樓呀？因為d有錢佬係到玩野呀，越有錢就越有得玩呀！呢個世界公平咩，呢個世界公平咩！」

片段是節錄自十年前 (1999) 無線電視劇《創世記》，近日在網絡上熱起來。

套用落十年後的今日，依然適用。還有甚麼話好說？好聽的講，香港「安定」吧，難聽的，就是無進步。

當年董伯伯本著惻隱之心，希望安得廣廈千萬家，但既得利益者眼看身家插水，當然同你死過。自此，政府很多事情咪照顧有錢佬。市民？不打緊啦，市民無乜能力令政府倒台，但有錢佬有這個能力，通北京關係良好的更加有這個能力。

大陸高官都識慢慢來。人仔一下急升的話，喪失廉價勞動力這優勢，佢都好唔掂，所以懶理美國佬吠，我有我慢慢升。但慢慢來不等於乜都唔做。

香港現在就係乜都唔做，甚至火上加油。或者咁樣，佢地懂活用慢慢來吧。普選！？慢慢來啦，哈哈哈哈)))))))))))) 2017 後來個 2022......

已發展地區貧富差距最大，這是美譽嗎？
唔駛理。幾百萬小市民，who care??最重要是19個億萬富翁！

在 youtube 重溫了一些創世紀精華片段，又幾好睇。當年我覺得創世紀都幾閹悶，特別係下部《創世記II之天地有情》。人大左，心態唔同？還是精華特別好睇？

不過我想 CCTVB 現在無可能出到這些精警對白。一來自我審查，二來香港越來越多道德塔利班。看 youtube，創世記中有一段出現「頂你個肺」，今時今日，相信無可能出街。

電視劇，越來越與社會脫節。七十二家租客？有無搞公呀。現在乜世紀？當年七十二家房客的成功在反映民生不態。在這個世紀沒有好題材嗎？幹麼要炒冷飯？？或者只當古裝片的延申……晚清、民初……之後咪到六七十年代 lor……

大刷膠

可以用的，不過這不是 Seed Radar，是冒牌貨？
不知道何時會用完呢？

OX

這公仔，黑色和白色的是同一個樣子，但我覺得黑色的精靈得多，白色的很呆。你覺得嗎？

派糖

無預過政府會派糖，就算派，幾年來的經驗，發覺最大得益者也不會是市民。
偏遠地區交通津貼？津貼給大欖隧道加價。
幼稚園學券？小型幼稚園結業，大規模的則加價。
注資入MPF？我無得益。最大得益也是保險公司吧，賺蝕都有錢收。
金融海嘯，我之前在mpf賺落的也倒蝕，又做左傻仔聽個代理講轉番保本先，結果回升無我份。每當看見紅色(代表蝕錢)的結算書，真是火上心頭。
送一百蚊慳電膽券？當初聽到都覺奇怪，要搞環保大把野好搞，大把新電器都慳電過舊電器，又安全d，倒不如資助貧窮老弱換新電器更好吧？又或者益下巴士公司，資助佢地換晒新車好過啦，果d舊車的廢氣真係恐怖。結果被揭發懷疑利益輸送。今次傳媒對特首好似鬆過甘乃威喎，唔係應該掉轉嗎？又一次看清傳媒。

買樓，我想這一世人都無乜本事。那個醫生+律師的一對，也供不起樓，或者是誇張了一些。但要搵幾多錢先供得起樓？
我供唔供得起？沒有認真計過。但我一家四口，就算預阿妹第時嫁出去，都無理由預自己孤獨終老吧？自己加埋老婆仔女加埋父母，起碼要預五六個人啦，無理由買兩三百呎掛？預五百呎吧。在天水圍也要一百萬。扣晒所有生活必要開支，勉強都可能得掛。但之後唔駛預自己會有乜娛樂。出街睇戲食飯？免問。旅行？發夢好啦。每個月辛辛苦苦賺來的，除了家用，就是奉獻給李生。仲有，要預家人自己來緊十幾廿年身壯力健。一個唔好彩有乜病，都唔知邊到搵錢來醫。一個唔該失業好幾個月，咁又點算？這個十幾廿年的重膽，我頂得住嗎？
衣食往行，這個「住」，得來不易。
有些人，說甚麼量力而為。無錢買市區，買新界。但這樣看來，莫講是新界，深圳河以北的都無本事買。無錢買樓？租樓lor！
無得著？有無得租衫？
無得食？租野食？？

Panorama

奧海公園，竟然沒有小朋友在玩耍？？






青衣公園觀景台，不過這日天氣差得很。




看似是90度的視野，其實這已經是270度了。

從畢氏定理說起

最近看書，引發我從另一個角度看畢氏定理。


大家還記得畢氏定理吧？參看圖中的直角三角形，畢氏定理指出了三邊的關係：「a^2 + b^2 = c^2」。
中學時大家做過不少習題，知道符合這關係的 (a, b, c) 的值，有可能是漂亮的整數，如 (3, 4, 5)，亦有可能不太漂亮，如 (2, 3, sqrt(13))。數學家對整數特別有興趣，把這些非零整數的 (a, b, c) 稱為 Pythagorean triples，如 (3, 4, 5), (5, 12, 13) 便是其中兩組。

現在我們把數式「a^2 + b^2 = c^2」變換一下。
把整個式子除以 c^2，得出
(a/c)^2 + (b/c)^2 = 1
設 x = (a/c), y = (b/c)，得出
x^2 + y^2 = 1
似曾相識嗎？無錯，這是圓方程。下圖的紅色線，顯示該方程在第一象限中的圖像。

每個符合畢氏定理的 (a, b, c)，均可化為該線上的一點。
而當中的 Pythagorean triples，便是該線上 x 坐標和 y 坐標均是非零有理數的點。
在數線上，不難想像任何兩個有理數之間，我們必定會找到無理數；任何兩個無理數之間，也可找到有理數。無理數與有理數，大家互相穿插其中。
平面上也應該差不多吧？
任意兩個有理的 x 坐標之間，必會出理無理的 x 坐標；任意兩個無理的 x 坐標之間，也必會出現有理的 x 坐標。
任意兩個有理的 y 坐標之間，必會出理無理的 y 坐標；任意兩個無理的 y 坐標之間，也必會出現有理的 y 坐標。
在 xy 平面上畫一條線，該線會通過一些 x, y 坐標均是有理數的點，不足為奇吧？
就像 x^2 + y^2 = 1 的圖像般。

真的嗎？
大家留意到圖中還有一條藍線吧？那是方程 x^3 + y^3 = 1 的圖像。
這條線也會通過一些 x, y 坐標均是非零有理數的點嗎？
答案是不會的。
點解？
費馬大定理
費馬大家理，幾百年前費馬的一個猜想，它猜測方程「a^n + b^n = c^n」當 n 是大於2的整數時，(a, b, c)不可能全是非零整數。這個猜想，一直到十多年前才得以證明。
把「a^n + b^n = c^n」全式除以 c^n，再如之前般設 x=a/c, y=b/c，得出
x^n + y^n =1。
若x, y 可以是有理數，把全式乘以 (x 和y 的 分母的 LCM)^n，便得可得出一組整數的 (a, b, c) 符合「a^n + b^n = c^n」，這與費馬大定理產生矛盾，所以是不可能的。
因此，
曲線 x^3 + y^3 =1 不會通過 x, y 坐標均是有理數的點。
曲線 x^4 + y^4 =1 不會通過 x, y 坐標均是有理數的點。
曲線 x^5 + y^5 =1 不會通過 x, y 坐標均是有理數的點。
.
.
.
只要 n 是大於 2 的整數，曲線 x^n + y^n =1 不會通過 x, y 坐標均是有理數的點。

神奇嗎？這兒有無數條曲線，都不會通過 x, y 坐標均是有理數的點！
雖然有理數、無理數均有無數個，但這樣看來，有理數與無理數相比，真是少得可憐。

數，是數論、代數問題。坐標，是幾何問題。很少會把兩者一併來看，是我的想像力太低吧。

如果 n 不是整數，例如 2.5, 3.334, 甚至是 sqrt(3)、Pi 等無理數，情況又會如何呢？我不知道。

靜夜思

床前明月光
疑是地上霜
舉頭望明月
低頭思故鄉

這首傳誦千古的《靜夜詩》，是有詩仙之稱的李白之經典作品。相信沒有一個中國人未曾聽過。

最近讀到一則舊聞，知道這個版本是在明、清開始流傳，再之前的版本是這樣的：
床前看月光
疑是地上霜
舉頭望山月
低頭思故鄉

不知這個版本是否李白的原作，但我覺得這個版本好得多。
以前我覺得「床前明月光」中的「明」，應作動詞，但又解不通。這個較古老的版本，看月光則通得多了。看那篇報導，還說一首詩出現兩次「明月」，不合格律。較古老的那個版本沒有這問題。

改完更差，點解明清學者要改李白的大作？真係唔知……

我覺得可能同方言有關。

以前看過一些文章，其實我們南方人用的漢語，保留了很多古漢語的音調、用字。年代月晚，我們中國的政治中心越往北移，可能因此令北方漢語有了優勢。試用普通話念那個較古舊版本的靜夜思，念起來不及新版動聽的。或許明清的學者就是這原因把詩改掉。

真不明白學中文點解要學普通話。現在小學生，上中文課也用普通話，頂！北大人控制了這個話語權。普通話咪又係方言，北京人的方言。去台灣的討論區如果打「香港文」，會比人圍剿，話你用外星文。其實很多台灣文我們也未必看懂。白話文=普通話？大把所謂白話文，一大堆北京土話，南方人也不會看得懂。

有一排流行國語唐詩光碟，賣晒廣告，但我覺得很難聽。念唐詩還是廣東話好聽得多。

堂堂偉人的大作都可改掉，讀到這舊聞不禁心傷。如果蒙娜麗莎的微笑出現在中國，幾百年後所流傳的會是惡搞版嗎？

無法啦，這就是命。

周秀娜

科大舉行「解構周秀娜現象」這講座(其實是解構還是解讀？我見一些媒體寫解讀，也有一些寫解構)，當知道會邀請周秀娜出席討論時，我就覺得這講座只是吹水綽頭成份居多。

我一直都想找個足本片段看看，不過找不到，算罷。

我想知道，教授眼中的「周秀娜現象」，指的為何物？是指這個夏天出現的一連串與o靚模有關的各種現象？各種現象好多喎，具體上來說是指哪些呢？還是只是針對周秀娜一人的出位言行？例如食雪糕、攬枕等這些在某些人眼中是意淫的東西？不知道在該講座內教授有沒有加以解釋？前提是甚麼也未搞清，之後都係晒氣。我見報章上沒有提及，不過大家都知娛樂版是甚麼吧，所以還想看看原片。

第二天的報紙，也是一面倒去插周秀娜，甚麼出醜呀、未夠班呀。我估佢本人都預左，反正又不是要建立才女形象。

傳媒的報導，主要是針對周秀娜的獻醜位。如唔識答，傻笑、「好深喎」、「可唔可以再問多次？」、「都係好深喎」。

我覺得那位教授，明知對方只是中學程度，就不應拋書包，講術語。這樣做分明是要人家當眾出醜。

很多媒體也彈這講座內容空洞。你知道點解嗎？我認為是邀請了周秀娜參與討論的原固。別誤會，我絕不是想說周秀娜本人未夠班、沒料子。我是想指責主辦單位純為搏出位搞宣傳，不理講座質素。一向我都覺得科大是幾所本地大學中最懂搞公關的一所，看來這次衰了。

打個比喻，如某講座題為「解讀金融海嘯」，大家預期會有甚麼講者？可能是一些大學金融系教授，可能係現職金融界的專業人士，但絕對不會請「金融海嘯」講兩咀吧？

你可能說金融海嘯無口呀，不是人呀。又如何？各「專業人士」也可盡情「客觀」地解讀。同樣地，周秀娜是這講座的焦點，但他是否講者，又有何干？要這個講座有內容，我認為請多幾位有料子、對社會現象有見地的人士，效果會好得多。

請周秀娜上台，講題很明顯由「解讀、解構」，變為「公審」。

若然周秀娜能夠答出一些很有深度的答案，同教授辱槍舌劍，在場幾百人很多都要好好反省。要知道部分大學生只想著打機溝女搵快錢啊，當然還要懂得抄 source，如果唔係點「過」呀。

(一講起 source，真係火都來。早幾天係大快活食飯，隔離台那個女仔同阿爸阿媽係到講就來 mid term 啦，不過都唔緊要，mid term 背 source 就行了。頂！應出卷的人懶去出卷，應求學的人懶去求學！看樣子該父親應該接受過大學教育，但無言以對，不知道當時有甚麼感想。)

周秀娜，或者他所屬的公司，可能有一些獨特見解，但佢無需要向你地解構自己吧。正如就算阿蘇去問人家的美食點整，可唔可以「解構」一下，人家都不會傾囊盡授。比別家對手洞識箇中秘密，市場價值可降低不少呢！

我個人點睇周秀娜？ She's hot, but not so beauty.
他亦是這場o靚模熱的眾多o靚模中，較多顯露自己個性的一位，其他大多只顯露乳房吧。就算同新進的歌影視姐仔相比，周秀娜亦是較有個性的一位，雖然很可能純是公司塑造出來，並不是他的真我。自我、獨立、有主見，是我眼中的周秀娜。

無論周秀娜的表現如何，我都對她增添兩分好感。明知是一場公審，明知不可為而為知，明知面對一場沒有 source 的測驗，明知第二日傳媒只會一面倒插自己，依然出席，實在很有勇氣。

Angelababy

在尖沙咀看見這個巨型海報。
每次行經 2% 我都會駐足觀看觀看，這個巨型的外牆版本還是第一次見。女角漂亮，紅撞綠這配搭應該很搶，但這照片看上去我覺得氣氛很和皆寧靜。

後來我才知道原來照片中的靚女就是人稱是「o靚界女神」的 Angelababy。死肥仔也為之著迷？非也非也。只是喜歡這海報罷了。

Burger Box

最近不知為何好想食漢堡包。去過 Pro Burger 後，過幾日我去比多一次機會 Mos Burger，試下其他款，依舊係唔好食。這次幫襯了中環7號碼頭的 Burger Box，正呀，合我口味，我覺得好食過 Pro Burger。薯條很正，夠薯味，Pro Burger 的我覺得太淡，而且口感太多油。肉，不及 Pro Burger 多汁，但肉味濃郁得多。

想再去食 Burger King。不過好幾次都見荃灣的很多人，還是去間較遠的，順道當是無聊逛逛。

炒

上文提到，我覺得渣打的150元紀念鈔短期內不會炒得起。事隔幾天，報章上已有報導說跌破官價。
官價$280，有錢幣店只售 $275。看來有些人原先預作短炒，看見短炒不行，急於套現吧。
熟算四連張和三十五連張，暫時也不是賺得多，與奧運鈔相差甚遠。
自己買了兩套，即是說蝕了 $10，哈哈哈……不打緊，我都無想過會放。
不過我想這套甚具歷史價值，長線來說一定有得升。可能留到自己的孫，會有可觀的回報。
一直覺得這類快錢不是我賺的。命水生成吧。買了幾年六合彩，連 $20 安慰獎也未曾中過，都算是經典。說實話，我未聽過有人買左幾年連$20都未中過。
投資？不敢呢。不清楚這遊戲，不懂去玩，不想辛苦錢眼白白無晒。就連強積金都可以咁玩我，真係 @$!!@%$@#
點解在這個社會，賺大錢，非要投機把賭不可。
我這種人，不會窮到餓死街頭，三餐不飽。但要享受豐盛的物質生活，不會輪到我。

150

買了渣打150元紀念鈔。

今日到奧海城看電影早場，購票後還有很多時間四圍逛，發現原來購買渣打150元紀念鈔的反應不太熱烈，於是我也買來紀念一番。

之前看報得知會發行150元紀念鈔，也有一些意欲購買留念，因為面值150元實在特別。不過想起去年中銀的奧運紀念鈔，排隊的人龍實在得人驚。那次我也想過購買普通版的，但不至於看見如斯人龍也願去排隊，更加不會益炒家。

這次渣打的，面值150元，說是甚麼全球首創，心想定必吸引很多排隊黨來掃貨炒賣，所以我都沒有想過會買成。誰知看見銀行門外架起作排隊之用的鐵欄，眼見有五六行，但只用到一行，於是我也去排隊輪候。很快便輪到我，現金交易，十分爽快。由排隊到收貨，過程快過去櫃員機提款。

在奧海城分店處，每次最多限買十套，但沒有限你排多少次。我見有些人應該排了好幾次，捧著一個大膠袋，內裏起碼有四五十套，買來炒賣嗎？但如此容易給我買到的東西，我想沒有甚麼短期的炒作潛力。

當我看完電影再去渣打望一望，已經不用排隊，要買的話真是快過去麥記買包！

可能是渣打這次安排得好，減低炒作之風。喜歡炒賣的人，可以一早應購甚麼自選號碼、幸運號碼、幾多幾多連張等。聞說35連張的炒價比定價高一倍，不知是否有價有市呢？而像我這種覺得特別只想拿來作一個紀念的市民，也可輕輕鬆鬆購買。炒家有炒家的喜，我有我的樂，實在皆大歡喜。加上今日職員親切友善，令我對渣打多了兩分好感。

渣打150週年，與我何干？只是對那面值150元感興趣。

京奧其實多幾分親切，但發行紀念鈔變成炒賣的貨品，去年看在眼裏實在火上心頭。或許是中共送給港人賺快錢的大禮。花時間排下隊，就必定有回報，好過去抽新股，更好過努力去工作。

如果當局真想與民同樂，印一批流通市面便可，鍾意直版的就去排隊。我又不太介意不是直版，如果購物、提款時收到，便留下一兩張留念，這也不錯。記得之前的97紀念硬幣也有流通市面，像 Laughing 哥的五蚊銀便是其中一枚。很多人也見過吧？

港人之樂，在於炒賣，中共也深明此道，投其所好。